【基本】和集合の要素の個数
ここでは、和集合の要素の個数を数える問題を見ていきます。【基本】集合の要素の個数では倍数の個数を数えましたが、これを応用した問題を考えます。
どちらかで割り切れるものの個数
「3または4で割り切れる」ということは、3で割り切れるものと4で割り切れるものをあわせたものになります。今の場合、具体的に書き出すと
3の倍数: 3, 6, 9, 12, 15 の5個
4の倍数: 4, 8, 12 の3個
であり、これを合わせると
「3, 4, 6, 8, 9, 12, 15」
の7個になります。ダブらないように、小さい方から順番に書き出すようにしています。こうして数えれば、7個が答えだとわかります。
ただ、今回のように毎回書き出すのは面倒です。もう少し簡単な出し方、計算だけで出す方法を考えてみます。
【基本】集合の要素の個数で見たように、割り算をして考えてみるとよさそうです。 $15\div3=5$, $15\div4=3.75$ なので、「3の倍数は5個、4の倍数が3個」だとわかります。ただし、 $5+3=8$ とただ足すだけではダメなようです。なぜなら、上のように書き出して数えると「7個」となるからです。なぜ、ただ足すだけではダメなんでしょうか。
それは、ダブっているものがあるからです。3の倍数と4の倍数を書き出したものの中に「12」がダブっています。両方の集合に入っているものは、2回数えることになってしまいます。なので、これを除かないといけません。
「3の倍数の集合に含まれ、4の倍数の集合にも含まれるもの」というのは、12の倍数のことです。12は3と4の最小公倍数ですね。 $15\div12=1.25$ なので、12の倍数は1個だけです。以上から\[ 5+3-1=7 \]個となり、書き出して数えたときと同じ結果になります。
ベン図で考えてみよう
集合を考えるときには、【基本】共通部分と和集合で見たように、ベン図を使うとわかりやすくなります。これを使って、上の例題をもう一度考えてみましょう。
例題では、「1から15までの整数」について考えました。この中で、3の倍数か4の倍数になっているものを数えるんでしたね。
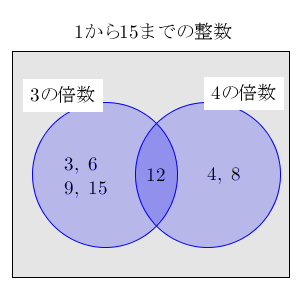
青い部分に含まれているものが対象なので、「7個」が答えになります。この「7」を求めるために、左側の円(3の倍数)にある「5個」と、右側の円(4の倍数)にある「3個」を足し、ダブって数えた中央部分(12の倍数)にある「1個」を引いて求めたんですね。
原理的には、細かい3つに分解しても求めることができます。つまり「3の倍数だが4の倍数でない」「3の倍数でも4の倍数でもある」「3の倍数でないが4の倍数」の3つの集合の要素数を求めて、すべて足してもかまいません。しかし、倍数の場合は、「あえてダブって足してから、ダブったところを引く」という数え方のほうが楽な場合が多いです。倍数の個数が簡単に求められるからです。ダブらせて数えた後でつじつまを合わせる方法は【標準】ダブらせて数えるでも見ましたが、倍数の問題でもよく使います。
記号を使ったまとめ
【基本】共通部分と和集合で見た通り、「集合 A または集合 B」という集合は和集合といって、 $A\cup B$ と書くんでしたね。また、両方の集合に属している要素を集めたものは共通部分といって $A\cap B$ と書くのでした。
この記号を用い、【基本】集合の要素の個数で紹介した通り、集合 A の要素を $n(A)$ で表すと、上で説明した内容から次が成り立つことがわかります。
\[ n(A\cup B) = n(A) +n(B) -n(A\cap B) \]
おわりに
ここでは、和集合の要素の個数を数える方法を見ました。少なくともどちらか一方に入っているものの個数を直接求めることは難しいことが多いのですが、それぞれの集合の個数を足して両方に入っている要素の個数を引けば出せる、というのはよく使うテクニックです。覚えておきましょう。





