🏠 Home / 数学II / 図形と方程式 / 軌跡

【基本】軌跡（連動して動く点）

🕒 2017/09/04 🔄 2023/05/01

ここでは、ある点と連動して動く点の軌跡を考えます。

📘 目次

連動して動く点

例題

円 $x^2+y^2=4$ 上を動く点 A と点 $\mathrm{ B }(4,0)$ の中点 P の軌跡を求めなさい。

A も P も動くので考えづらいですが、答えは想像しやすいと思います。

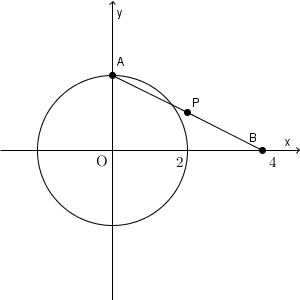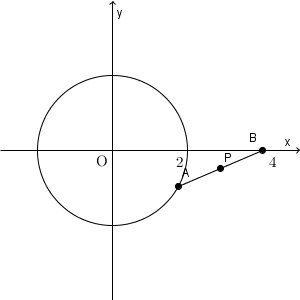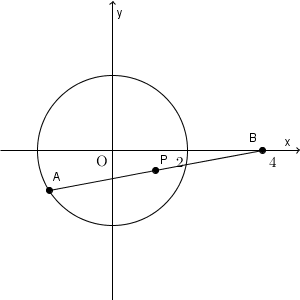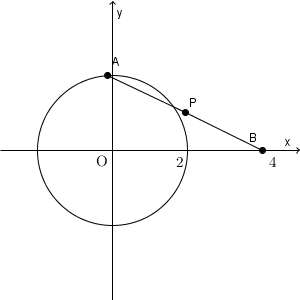
これも、基本的には、【基本】軌跡（垂直二等分線や角の二等分線）などで見たように、 $\mathrm{ P }(X,Y)$ などとおいて、 X, Y が満たす関係式を見ることになります。

ただ問題なのは、 A が動いていることなんですよね。 A の座標が固定されていません。なので、こちらも文字で置く必要があります。 A の座標を $(s,t)$ とおくことにしましょう。

こうすれば $\mathrm{ A }(s,t)$, $\mathrm{ B }(4,0)$ の中点 P の座標は\[ \left(\frac{s+4}{2},\frac{t}{2}\right) \]となることがわかるので、\[ X=\frac{s}{2}+2, Y=\frac{t}{2} \]という関係式が成り立つことがわかります。

ただ、これだけを見ても、 X, Y がどんな関係式を満たすのか、 P の軌跡がどうなっているのかはわかりませんね。 s, t が邪魔です。今まで見た【基本】軌跡（垂直二等分線や角の二等分線）などの例では、 X, Y の関係式がすぐに出てきましたが、この例題ではすぐにはわからない、という点が違います。

さて、 s, t が邪魔なので消したいのですが、これはそもそも何だったかを思い出してみましょう。 A の座標ですね。そして、 A は何だったかというと、円 $x^2+y^2=4$ 上を動く点です。なので、次の式が成り立ちます。\[ s^2+t^2=4 \]円上の点だから当たり前ですね。

この式と、先ほどの\[ X=\frac{s}{2}+2, Y=\frac{t}{2} \]を見比べてみましょう。これらの式を組み合わせれば、 s, t がうまく消せることがわかります。まず、次のように変形します。\[ s=2X-4, t=2Y \]そして、これを先ほどの円の式に入れると
\begin{eqnarray} s^2+t^2 &=& 4 \\[5pt] (2X-4)^2+(2Y)^2 &=& 4 \\[5pt] 4(X-2)^2+4Y^2 &=& 4 \\[5pt] (X-2)^2+Y^2 &=& 1 \\[5pt] \end{eqnarray}となります。うまい具合に、 X, Y に関する式が出てきました。これより、 P は円 $(x-2)^2+y^2=1$ 上にあることがわかります。

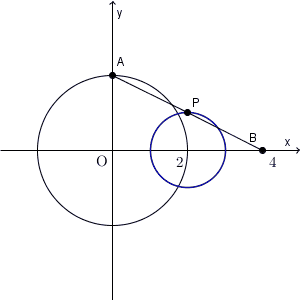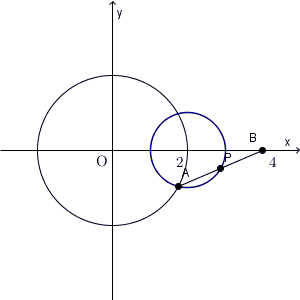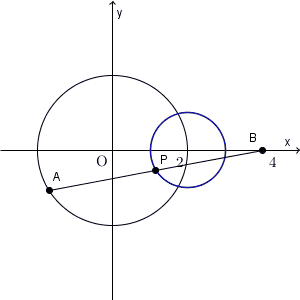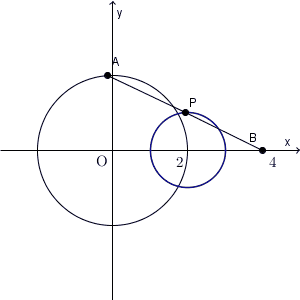
逆に、 P がこの円上にある場合、対応する A が存在し、条件を満たすことがわかります。なので、求める軌跡は、「円 $(x-2)^2+y^2=1$ 」となります。

「ある動く点に連動して動く点の軌跡」を求める問題は、少し難易度が高いです。たいていの場合は、上の例題と似た流れで解きます。まず2つの動く点の関係式を求めます。そして、基準となる点（上の例題で言えば点 A ）に関する式に代入して、求めたい軌跡の方程式を求めます。最後に、すべての点が条件を満たすことをチェックします。

もし、条件を満たさない点があれば、それらを除いて答えなくてはいけません。そのような例題は、また別の機会で取り上げることにします。