【基本】極限値と微分係数
ここでは、極限値を用いて、微分係数の定義を見ていきます。
微分係数の復習
【導入】微分を考える意味についてで見たように、三次関数などのグラフをかくには、いくつかの点をつなぐだけではダメで、新しい手法が必要なのでした。そして、【基本】平均変化率で見たように、 x の変化量で y の変化量を割った「平均変化率」を用いれば、 x が変化したときに y がどのように(平均的に)変化するかがわかるのでした。
ただ、この「平均変化率」は、 x の変化が大きすぎると問題があるのでしたね。そこで、【基本】微分係数で見たように、 x の変化量をすごく小さくしていったときの平均変化率=微分係数が使えそうだ、というところまでを見ました。
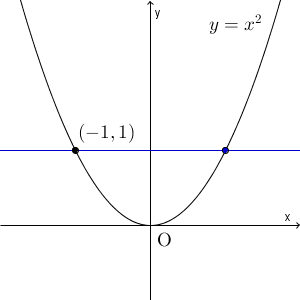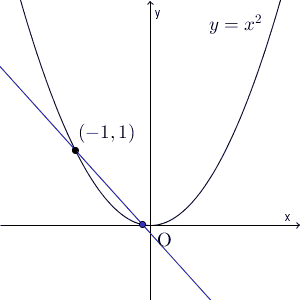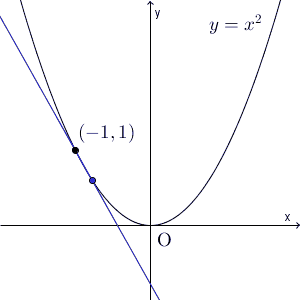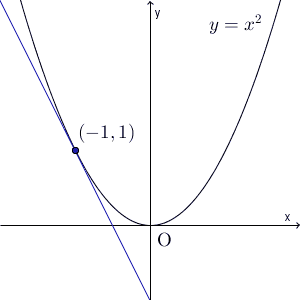
上の図は、 $y=x^2$ に対し、 $x=-1$ から $x=b$ までの平均変化率がどう変わっていくかを表したものです。区間の右端 $b$ を $-1$ に近づけていくと、平均変化率(青い直線の傾き)は、ある値に近づいていくことがわかります。この値のことを微分係数というのでしたね。具体的な値は、【基本】微分係数で計算しましたが、 $-2$ となります。
ここで出てきた「ある値に近づいていく」などということを、数学では、次で説明するように、「極限値」というものを使って表現します。
極限値
一般的な関数 $f(x)$ があったとします。これは、 $f(x)=x^2$ でも何でもいいのですが、一般的な関数を使いたいときは、関数 function の頭文字を使って $f(x)$ と表すことが多いので、ここでもこれを使います。
関数 $f(x)$ に対し、 x が a と異なる値をとりながら a に限りなく近づくときに、もし $f(x)$ が $\alpha$ というある値に近づくとき、\[ \lim_{x\to a}f(x)=\alpha \]と表します。「 $x\to a$ 」が「 x が a に限りなく近づくこと」を表しています。
また、このときの $\alpha$ のことを、「 $x\to a$ としたときの $f(x)$ の極限値(limit value) といいます。記号の $\lim$ は limitの略です。
「 $\to$ 」が「限りなく近づく・近づける」を意味するので、上のことを「 $x\to a$ のとき、 $f(x)\to\alpha$ 」などと書くこともあります。
例えば、\[ \lim_{x\to 1}x^2 \]はどうなるかというと、 x が $1$ に限りなく近づけば、 $x^2$ はもちろん $1$ に近づくので、\[ \lim_{x\to 1}x^2=1 \]となります。
また、\[ \lim_{x\to 0}\frac{x^2-2x}{x} \]はどうなるでしょうか。 x が $0$ に限りなく近づけば、分母も分子も $0$ に近づいて行ってしまいます。このままだと値がどうなるかわかりづらいですが、約分してから考えればわかりやすいですね。\[ \lim_{x\to 0}\frac{x^2-2x}{x}=\lim_{x\to 0}(x-2)=-2 \]となります。
極限値と微分係数
さて、「限りなく近づける」ことを数学の世界でどう書くかを見たので、微分係数の定義を書き直してみましょう。
微分係数とは、平均変化率の式で、 x の変化量を限りなく $0$ になるようにしたものでしたね。 x が $a$ から $b$ まで変化したときの平均変化率は\[ \frac{f(b)-f(a)}{b-a} \]です。 $x=a$ での微分係数は、 b を a に限りなく近づけたものなので、\[ \lim_{b\to a}\frac{f(b)-f(a)}{b-a} \]が微分係数となります(冒頭の $f(x)=x^2$ と $a=-1$ だと対応させながら考えてみましょう)。これが、極限値を用いた微分係数の定義です。
また、同じことですが、「 $b$ を $a$ に近づける」ではなく「 $b-a$ を $0$ に近づける」と考えることもあります。差が $0$ に近づくことと同じだから、同じものを指すことになります。 $b-a=h$ とすると、次のように変わります。\[ \lim_{h\to 0}\frac{f(a+h)-f(a)}{h} \]これも、微分係数です。どちらも同じ意味の式ですが、こちらが使われることが多いです。
「 $f(x)$ の $x=a$ での微分係数」という言葉は長いし、 $\lim$ を使った式も長いので、これをシンプルに $f'(a)$ という記号で表します。 $f$ の右上にあるものが「微分係数」の証です。
最後に、冒頭で見た例を具体的に計算してみましょう。 $f(x)=x^2$ の $x=-1$ での微分係数は
\begin{eqnarray}
& &
\lim_{h\to 0}\frac{(-1+h)^2-(-1)^2}{h} \\[5pt]
&=&
\lim_{h\to 0}\frac{h^2-2h}{h} \\[5pt]
&=&
\lim_{h\to 0}(h-2) \\[5pt]
&=&
-2 \\[5pt]
\end{eqnarray}と求められます。後半で出てきた極限値の計算は、先ほどの極限値の計算例でも出ている内容です。
おわりに
ここでは、極限値の定義を紹介し、極限値を使って微分係数の定義を書き直しました。この定義の式は、微分の世界では最も基本的で重要な式なので、よく覚えておきましょう。微分の話は、すべてこの定義式から出発します。





