【基本】ベクトルの内積と成分
ここでは、ベクトルの成分を使って、ベクトルの内積を表す方法を見ていきます。
ベクトルの内積の復習
$\vec{0}$ でない2つのベクトル $\vec{a}$, $\vec{b}$ があって、この2つのベクトルのなす角を $\theta$ としたとき、内積は\[ \vec{a}\cdot \vec{b} = |\vec{a}||\vec{b}|\cos\theta \]と定義するんでしたね(参考:【基本】ベクトルの内積)。
ただ、この定義だと、なす角がわからないと内積がわかりません。図形問題などでは、角度が分からないことも多いので、これだけだとわざわざ内積を考える意味がありません。
しかし、このすぐ後で見るように、ベクトルの成分を使えば、ベクトルの内積を簡単に表すことができます。なので、成分から内積を求め、なす角を求める、といった使い方ができるようになります。
以下の説明では、三角比で学んだ、余弦定理を使います。不安な人は、【基本】余弦定理の基本的な使い方などを見直してみましょう。なお、内積の定義に $\cos$ が出てくることからもわかる通り、内積を使う問題では三角比で学んだ内容を使うことがあります。 $\cos$ を見てイヤな予感がした人は、三角比の内容を復習しておくのもいいかもしれません(一応、直接使うものは、その都度リンクを貼る予定です)。
ベクトルの内積と成分
さて、ベクトルの成分を使って、内積を表す方法について考えていきましょう。
$\vec{0}$ でない2つのベクトル $\vec{a}=(a_1,a_2)$, $\vec{b}=(b_1,b_2)$ について考えます。
これらのベクトルに対し、始点を合わせて、始点を O とし、 $\overrightarrow{ \mathrm{ OA } }=\vec{a}$, $\overrightarrow{ \mathrm{ OB } }=\vec{b}$ となるように、 A, B をとります。また、なす角は $\theta$ とおきます。
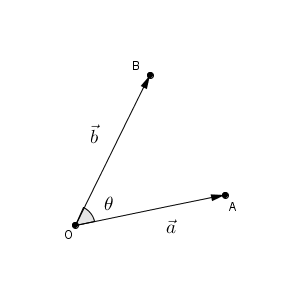
$\theta$ が $0^{\circ}$ でも $180^{\circ}$ でもないとき、三角形 OAB に対して余弦定理が成り立つので、
\begin{eqnarray}
\mathrm{ AB }^2
&=&
\mathrm{ OA }^2+\mathrm{ OB }^2-2\mathrm{ OA }\cdot\mathrm{ OB }\cos\theta
\end{eqnarray}が成り立ちます。ここでよく見ると、実は最後の部分に内積が出てきているんですね。 $\mathrm{ OA }\cdot\mathrm{ OB }\cos\theta$ というのは、ベクトルの言葉で書けば $|\vec{a}||\vec{b}|\cos\theta$ です。つまり、 $\vec{a}\cdot\vec{b}$ です。また、他の長さは成分を使って書くことができます。そのため、
\begin{eqnarray}
(b_1-a_1)^2+(b_2-a_2)^2
&=&
(a_1^2+a_2^2)+(b_1^2+b_2^2)-2 \vec{a}\cdot\vec{b} \\[5pt]
-2a_1b_1-2a_2b_2
&=&
-2 \vec{a}\cdot\vec{b} \\[5pt]
\vec{a}\cdot\vec{b}
&=&
a_1b_1+a_2b_2 \\[5pt]
\end{eqnarray}となります。成分を使って、こんなにシンプルな式で表現できるんですね。
最後に、例外的な場合について考えましょう。 $\theta=0^{\circ},180^{\circ}$ のときは、【標準】ベクトルの成分と平行で見た通り、 $\vec{b}=k\vec{a}$ となる k が存在するんでしたね。
$\theta=0^{\circ}$ のときは、 k は正、 $\theta=180^{\circ}$ のときは、 k は負、なので、どちらの場合も、
\begin{eqnarray}
\vec{a}\cdot\vec{b}
&=&
|k|\cos\theta \times |\vec{a}|^2 \\[5pt]
&=&
k|\vec{a}|^2 \\[5pt]
\end{eqnarray}です。また、\[ a_1b_1+a_2b_2 = k(a_1^2+a_2^2) \]なので、このときも\[ \vec{a}\cdot\vec{b}=a_1b_1+a_2b_2 \]が成り立ちます。
また、どちらかが $\vec{0}$ の場合、内積は $0$ となり、 $a_1b_1+a_2b_2=0$ も成り立つので、やはり、\[ \vec{a}\cdot\vec{b}=a_1b_1+a_2b_2 \]が成り立ちます。
以上から、どんな場合でも次が成り立つことがわかります。
例えば、 $\vec{a}=(2,1)$, $\vec{b}=(1,-1)$ なら、この内積は\[ \vec{a}\cdot\vec{b}=2\cdot1+1\cdot(-1)=1 \]と求められる、ということです。
これは、成分が分かれば内積が計算できることを表しており、これを使えばなす角(の $\cos$ の値)も簡単に求められることを示唆しています。角の求め方は、また別の機会に見ていきましょう。
おわりに
ここでは、ベクトルの成分を使って内積を表現する方法を見ました。成分同士を掛けて足すと、内積になるんですね。内積の問題ではよく使うので、マスターしておきましょう。