【基本】双曲線の焦点(焦点がx軸上)
ここでは、ある2点からの距離の差が0でない一定の値となる点の軌跡を見ていきます。
双曲線の焦点
【基本】楕円の焦点(焦点がx軸上)の場合とは異なり、今度は「距離の差が一定」となっています。【基本】双曲線の焦点(具体例)では、焦点が x 軸上にはなかったですが、今回は x 軸上にある状況で、一般化したものになっています。
さて、点 $(x,y)$ がこの軌跡上にあるとすると、次が成り立ちます。
\begin{eqnarray}
\sqrt{(x+p)^2+y^2}-\sqrt{(x-p)^2+y^2} = \pm 2a
\end{eqnarray}差が $2a$ なので、符号は両方考えられます。以降は、複号同順で考えていきます。
2つ目のルートを右辺に移項すると
\begin{eqnarray}
\sqrt{(x+p)^2+y^2} = \pm 2a+\sqrt{(x-p)^2+y^2} \quad\cdots(A)
\end{eqnarray}となります。ここで、両辺を2乗すれば
\begin{eqnarray}
(x+p)^2+y^2 &=& 4a^2 \pm 4a\sqrt{(x-p)^2+y^2}+(x-p)^2+y^2 \\[5pt]
4xp &=& 4a^2\pm 4a\sqrt{(x-p)^2+y^2} \\[5pt]
xp-a^2 &=& \pm a\sqrt{(x-p)^2+y^2} \quad\cdots(B)
\end{eqnarray}となります。さらに2乗して
\begin{eqnarray}
x^2p^2 -2a^2xp+a^4 &=& a^2(x-p)^2 +a^2y^2 \\[5pt]
(p^2-a^2)x^2 -a^2y^2 &=& a^2(p^2-a^2) \\[5pt]
\end{eqnarray}となります。ここで、 $p\gt a \gt 0$ なので、 $b=\sqrt{p^2-a^2}$ とおけば、この式は
\begin{eqnarray}
b^2x^2-a^2y^2 &=& a^2b^2 \\[5pt]
\frac{x^2}{a^2}-\frac{y^2}{b^2} &=& 1 \\[5pt]
\end{eqnarray}となります。
逆に、この式が成り立っているときに、条件を満たしていることを確認してみましょう。式を逆にたどっていくと、2乗している箇所が2か所あります。 $(A),(B)$ の部分です。
まず、 $(B)$ ですが、ここは両方の符号がついているので、同値な変形となっているため問題ありません。
続いて $(A)$ について考えます。 $x\gt0$ の場合、 $(A)$ の式内の $\pm2a$ はプラスの方に対応するので、両辺とも正になります。 $x\lt0$ の場合は、 $\pm2a$ のマイナスの方に対応します。このとき、 $x\leqq -a$ なので
\begin{eqnarray}
& &
-2a+\sqrt{(x-p)^2+y^2} \\[5pt]
&\geqq&
-2a+\sqrt{(-a-p)^2+0^2} \\[5pt]
&=&
-2a+a+p \\[5pt]
&=&
p-a \\[5pt]
\end{eqnarray}となります。 $p\gt a$ なので、これも正です。つまり、 $(A)$ も両辺は正になるので、式変形を逆にたどっていくことができます。
以上から、 $\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2} = 1$ を満たすすべての点が、条件を満たすことがわかりました。なので、これが答えです。
一般的に、「ある2点からの距離の差が、0でない一定の値になる点の集まり」を、双曲線(hyperbola) といいます。過去に見たことのある $y=\dfrac{a}{x}$ という式とはまったく違う形ですが、焦点の位置が違うだけで、 $y=\dfrac{a}{x}$ もこの性質を満たしています。特殊なケースについては、【基本】双曲線の焦点(具体例)で扱いましたが、一般的にも成り立ちます(このことは別の機会に見ていくことにします)。
この2点のことを、双曲線の焦点(focus) といいます。途中で、 $b=\sqrt{p^2-a^2}$ とおきましたが、これを変形すれば $p=\sqrt{a^2+b^2}$ となります。焦点の座標はこれを使って次のように表すことができます。
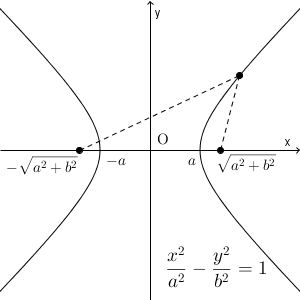
2つの焦点からの距離の差は $2a$ になります。中心は原点、頂点は $(-a,0)$, $(a,0)$ となります。用語は、【基本】双曲線の焦点(具体例)で扱っています。
おわりに
ここでは、双曲線について見てきました。今まで見てきた $y=\dfrac{a}{x}$ とは見た目が違いますが、これも上で見た定義に含まれています。
楕円とよく似た式が出てきますが、違いに注意しましょう。





