【基本】双曲線の焦点(具体例)
ここでは、具体的な双曲線の例を使って、双曲線を図形的に見ていくことにします。
ある2点からの距離の差が一定
【基本】楕円の焦点(具体例)や【基本】楕円の焦点(焦点がx軸上)などで見た通り、「ある2点からの距離の和が一定となる点の集まり」を楕円というのでしたね。【基本】楕円の方程式と円の方程式で見た通り、楕円は円を一方向に拡大・縮小した図形でした。

では、「ある2点からの距離の差が一定となる点の集まり」はどういう図形になるでしょうか。和ではなく、今度は「差」です。この図形はすでに見たことのある図形になります。具体的な例を通してみていきましょう。
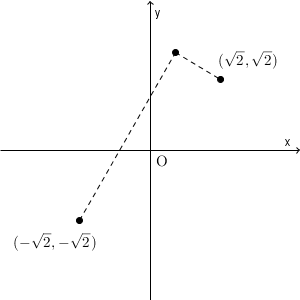
$(x,y)$ がこの軌跡上にあるとしましょう。すると、以下の式が成り立ちます。
\begin{eqnarray}
\sqrt{(x-\sqrt{2})^2+(y-\sqrt{2})^2}-\sqrt{(x+\sqrt{2})^2+(y+\sqrt{2})^2} &=& \pm 2\sqrt{2}
\end{eqnarray}差が $2\sqrt{2}$ なので、符号は両方考えられます。以下では、複号同順で考えていきます。
2つ目のルートを右辺に移項して両辺を2乗すると
\begin{eqnarray}
(x-\sqrt{2})^2+(y-\sqrt{2})^2 &=& 8 \pm 4\sqrt{2}\sqrt{(x+\sqrt{2})^2+(y+\sqrt{2})^2} +(x+\sqrt{2})^2+(y+\sqrt{2})^2 \\[5pt]
-4\sqrt{2}x-4\sqrt{2}y &=& 8 \pm 4\sqrt{2}\sqrt{(x+\sqrt{2})^2+(y+\sqrt{2})^2} \\[5pt]
x+y+\sqrt{2} &=& \mp \sqrt{(x+\sqrt{2})^2+(y+\sqrt{2})^2} \\[5pt]
\end{eqnarray}となります。
さらに2乗して
\begin{eqnarray}
(x+y+\sqrt{2})^2 &=& (x+\sqrt{2})^2+(y+\sqrt{2})^2 \\[5pt]
2xy &=& 2 \\[5pt]
y &=& \dfrac{1}{x} \\[5pt]
\end{eqnarray}となり、昔見たことのある、双曲線の式が出てきましたね。
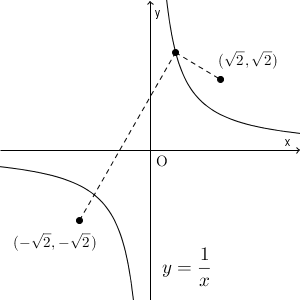
逆に、 $(x,y)$ がこの式を満たしているとしましょう。このとき
\begin{eqnarray}
& &
\sqrt{(x-\sqrt{2})^2+(y-\sqrt{2})^2} \\[5pt]
&=&
\sqrt{x^2-2\sqrt{2}x+2+\frac{1}{x^2}-\dfrac{2\sqrt{2} }{x}+2} \\[5pt]
&=&
\sqrt{\left(x+\frac{1}{x}\right)^2-2\sqrt{2}\left(x+\frac{1}{x}\right)+2} \\[5pt]
&=&
\sqrt{\left(x+\frac{1}{x}-\sqrt{2}\right)^2} \\[5pt]
&=&
\left| x+\frac{1}{x}-\sqrt{2} \right| \\[5pt]
\end{eqnarray}であり、同様に
\begin{eqnarray}
& &
(x+\sqrt{2})^2+(y+\sqrt{2})^2 \\[5pt]
&=&
\left| x+\frac{1}{x}+\sqrt{2} \right| \\[5pt]
\end{eqnarray}が成り立ちます。ここで、 $x\gt 0$ なら、相加相乗平均の関係から $x+\dfrac{1}{x}\geqq 2$ なので、この2つの差は
\begin{eqnarray}
& &
\left| x+\frac{1}{x}-\sqrt{2} \right| -\left| x+\frac{1}{x}+\sqrt{2} \right| \\[5pt]
&=&
\left( x+\frac{1}{x}-\sqrt{2} \right) -\left( x+\frac{1}{x}+\sqrt{2} \right) \\[5pt]
&=&
-2\sqrt{2} \\[5pt]
\end{eqnarray}となります。また、 $x\lt 0$ のときは、対称性から、差は $2\sqrt{2}$ になることがわかります。つまり、この双曲線上のすべての点は、条件を満たす、ということです。よって、\[ y=\frac{1}{x} \]が求める軌跡となります。
「ある2点からの距離の差が0でない一定の値となる点の集まり」を双曲線といいます。差が0の場合は、垂直二等分線になってしまうので除いています。一般的な場合については、別の機会で見ていくことにします。
この2点のことを焦点(focus) といいます。また、2つの焦点の中点を、双曲線の中心といいます。2つの焦点を結んだ線と双曲線とが交わる点を双曲線の頂点といいます。
おわりに
ここでは、具体的な例を用いて、「ある2点からの距離の差が0でない一定の値となる点の集まり」が今まで見たことのある「双曲線」になることを見ました。一般的な場合は、別の機会に見ていくことにします。





