【基本】楕円の焦点(具体例)
ここでは、ある2点からの距離の和が一定となる点の軌跡を見ていきます。
ある2点からの距離の和が一定
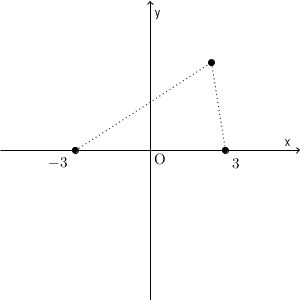
点 $(x,y)$ が条件を満たすとすると
\begin{eqnarray}
\sqrt{(x+3)^2+y^2}+\sqrt{(x-3)^2+y^2} &=& 10 \\[5pt]
\sqrt{(x+3)^2+y^2} &=& 10-\sqrt{(x-3)^2+y^2} \quad \cdots (A)
\end{eqnarray}となります。 $\sqrt{(x-3)^2+y^2}$ を移行して両辺を2乗すると
\begin{eqnarray}
(x+3)^2+y^2 &=& 100-20\sqrt{(x-3)^2+y^2}+(x-3)^2+y^2 \\[5pt]
12x &=& 100-20\sqrt{(x-3)^2+y^2} \\[5pt]
25-3x &=& 5\sqrt{(x-3)^2+y^2} \quad \cdots (B)
\end{eqnarray}となります。さらに2乗すると
\begin{eqnarray}
625-150x+9x^2 &=& 25(x-3)^2+25y^2 \\[5pt]
625-150x+9x^2 &=& 25x^2-150x+225+25y^2 \\[5pt]
400 &=& 16x^2+25y^2
\end{eqnarray}となります。両辺を $400$ で割れば
\begin{eqnarray}
\frac{x^2}{25}+\frac{y^2}{16} &=& 1 \quad \cdots (*)
\end{eqnarray}となります。
逆に、この式(*) を満たせば、条件を満たすことを確認しましょう。上の式変形を逆にたどっていけば、まず $(B)$ の部分で2乗しています。しかし、式(*)を満たしていれば、 $|x|\leqq 5$ だから、 $(B)$ の両辺は正であることがわかります。
また、さらに逆にたどっていくと、 $(A)$ の部分でも2乗しています。式(*)を満たしていれば、 $|x|\leqq 5$, $|y|\leqq 4$ だから、 $(A)$ の右辺のルートの部分は
\begin{eqnarray}
& &
\sqrt{(x-3)^2+y^2} \\[5pt]
&\leqq&
\sqrt{x^2-6x+9+4^2} \\[5pt]
&\leqq&
\sqrt{5^2+6\cdot 5+25} \\[5pt]
&\leqq&
\sqrt{80} \\[5pt]
&\lt&
10 \\[5pt]
\end{eqnarray}なので、 $(A)$ の両辺も正であることがわかります。
以上から、式を逆にたどっていくことができるので、求める軌跡は\[ \frac{x^2}{25}+\frac{y^2}{16} = 1 \]を満たす点全体、となります。
具体的に図形をかくと、次のようになります。
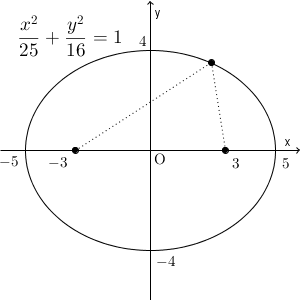
このような形を、楕円といいます。一般に、ある2点からの距離の和が一定の点の集まりを、楕円といいます。上は具体的な例で見ましたが、一般的な場合は別のところで見ていくことにします。
この2点には、焦点(focus) という名前がついています。上の例では、 $(-3,0)$, $(3,0)$ が焦点ということです。
この2つの焦点を結んだ直線のうち、楕円に含まれる部分を長軸といいます。また、長軸の垂直二等分線のうち、楕円に含まれる線分を短軸といいます。上の例でいえば、長軸の長さは $10$ で、短軸の長さは $8$ となります。
また、長軸と短軸の交点を楕円の中心、長軸と短軸の端点を楕円の頂点といいます。
楕円というと、円を、ある方向に拡大・縮小したもの、と考える人もいるかもしれません。実際、その性質もあるのですが、それについてはまた別のところで見ます。
おわりに
ここでは、具体的な例を使って、楕円の方程式を導きました。一般の場合は、別の機会に見ていくことにします。





