【基本】楕円の方程式と円の方程式
ここでは、楕円の方程式と円の方程式を使って、楕円と円の図形的な関係を見ていきます。
焦点がy軸上にある楕円
【基本】楕円の焦点(焦点がx軸上)や【基本】楕円の焦点(焦点がy軸上)で見たように、 $\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$ のグラフは、楕円となります。下の図の赤いグラフは $a\gt b\gt 0$ のときの楕円の例です。

また、原点を中心とし、半径が $a$ の円の方程式は $x^2+y^2=a^2$ であり、これは $\dfrac{x^2}{a^2}+\dfrac{y^2}{a^2}=1$ と変形できます。楕円の方程式とすごく似ていますね。
x 座標が $t$ のときの、それぞれの y 座標を求めてみましょう。対称性があるので、 x 座標も y 座標も、0以上の部分だけを考えればいいですね。
楕円の場合、 y 座標は次のようになります。\[ b\sqrt{1-\dfrac{t^2}{a^2} } \]一方、円のほうは、次のようになります。\[ a\sqrt{1-\dfrac{t^2}{a^2} } \]ルートの中は同じなので、楕円の y 座標は、円の y 座標を $\dfrac{b}{a}$ 倍したものであることがわかりますね。

x 座標がどんな場合でもこのことが成り立つので、以下のことが言えます。
円は楕円の特別な場合である
楕円 $\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$ は、 $a\gt b \gt 0$ なら、円 $x^2+y^2=a^2$ を y 軸方向に $\dfrac{b}{a}$ 倍に縮小したもの、 $b\gt a \gt 0$ なら y 軸方向に $\dfrac{b}{a}$ 倍に拡大したもの、ということがわかりました。このことから、円は楕円の特別な場合である、調和のとれた形である、と考えることができます。 $a=b$ のときですからね。
ところで、楕円とは、そもそも「2つの焦点からの距離の和が一定の点の集まり」でしたね。 $a\gt b\gt 0$ のとき、2つの焦点の座標は $(-\sqrt{a^2-b^2},0)$, $(\sqrt{a^2-b^2},0)$ と書くことができました(参照:【基本】楕円の焦点(焦点がx軸上))。このとき、 $b$ を $a$ に近づけていったときに、楕円や焦点がどのように変化していくかを見てみましょう。
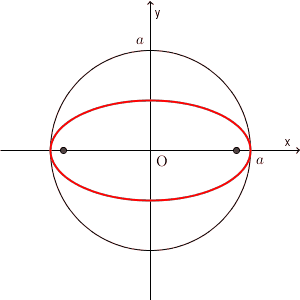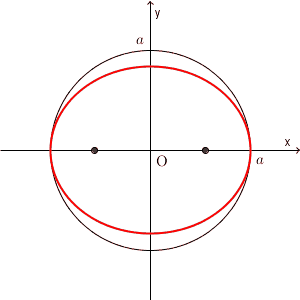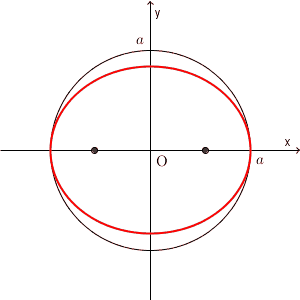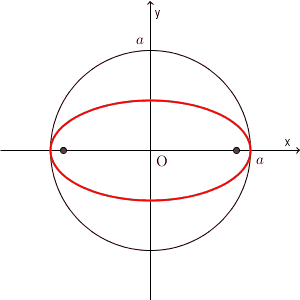
上の図は、 $b$ を変化したときに、楕円や焦点がどう変化するかを表しています。 $b$ が $a$ に近づくにつれて、楕円は円に近づいていき、 $b=a$ のときに、一瞬だけ円になります。また、このときに焦点( x 軸上を動いている2点です)は、両方とも原点にいることがわかります。
つまり、円の中心は、楕円の2つの焦点が一致した場合であると考えられます。「2つの焦点からの距離が一定」というのは、半径の2倍のことになります。
おわりに
ここでは、楕円と円の方程式から、楕円が円を一方向に拡大縮小した図形であることをみました。また、円が楕円の特別な場合と考えられることも見ました。





