【基本】微分係数

🕒 2017/10/05 🔄 2023/05/01

ここでは、平均変化率の考えをさらに発展させて、グラフの山や谷の部分を見つけるのに役立つ、微分係数の紹介をしていきます。

📘 目次

平均変化率の復習

【基本】平均変化率に引き続き、 $y=x^2$ について考えましょう。このグラフは次のようになります。

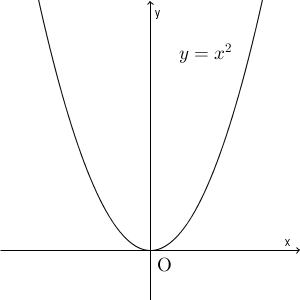
x が増えていくとき、原点までは y は減り続け、原点以降は増え続けますね。このような、 x の変化の仕方と y の変化の仕方との関係を見るために、平均変化率というのが使えるのでした。 x が a から b まで変化するとき、 y が A から B まで変化するなら、このときの平均変化率は、\[ \frac{B-A}{b-a} \]と書くのでしたね。これは、 $(a,A)$ と $(b,B)$ を結んだ直線の傾き、と言い換えることもできます。

例えば、 x が $-2⇒-1$ と変化すれば、 y は $4⇒1$ となるので、平均変化率は $-3$ です。だから、「平均的に見れば、下がっていくんだな」ということがわかります。また、 x が $1⇒2$ と変化すれば、 y は $1⇒4$ となり、平均変化率は $3$ なので、「平均的に見れば、上がっていくんだな」ということがわかります。これらはグラフともあっています。

下がっていく区間があり、その後で上がって行く区間があるので、その間に谷がある、と予想できます。

しかし、平均変化率はあくまでも、「考えている範囲で、平均的にどう変化するか」が分かるだけなんですよね。例えば、 x が $-1⇒1$ と変化すれば、 y は $1$ のままなので、平均変化率は $0$ です。「平均的に見れば、変化なし」なのですが、実際には y の値は動いています。

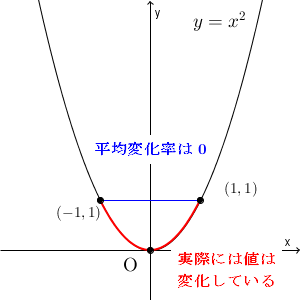
つまり、この場合、平均変化率を見ても、「 $x=-1$ 付近では、 x が増えるたびに、 y が減る」とか、「 $x=1$ 付近では、 x が増えるたびに、 y も増える」ということがわからないんですね。

平均変化率は、 x の変化量と y の変化量を比べているものですが、そのまま使っても、「 x が変化したときに y がどう変化するか」がわからないこともあるんですね。

微分係数

先ほど、平均変化率だけを見ても、「 x が変化したときに y がどう変化するか」がわからないこともある、と書きました。上の例を見ながら、なぜわからなかったかを考えると、原因に気づく人もいるでしょう。

それは、「考えている区間が広すぎたから」です。 $-1⇒1$ ではなく、 $-1⇒0$ や $-1⇒0.5$ などという区間で考えていれば、平均変化率はマイナスとなり、「 $x=-1$ 付近では、 x が増えるたびに、 y が減る」ことと合うようになります。

また、 $-1⇒1$ ではなく、 $0⇒1$ や $-0.99⇒1$ などという区間で考えていれば、平均変化率はプラスとなり、グラフからわかる「 $x=1$ 付近では、 x が増えるたびに、 y も増える」ことと合うようになります。

区間が広すぎるとダメなんですね。山付近、谷付近だと、すごく区間を狭くしないといけないことがわかります。しかし、「広すぎるかどうか」というのは、判断しづらいです。「区間が広い」の定義があいまいですからね。

そのため、「はじめから区間をものすごく狭くしておけばいいのではないか」という発想が出てきます。例えば、 $y=x^2$ で $x=-1$ 付近について考えてみましょう。 $-1⇒1$ という区間をどんどん狭めていったときに、平均変化率（2点を結んだ直線の傾き）がどう変わっていくかを見てみましょう。

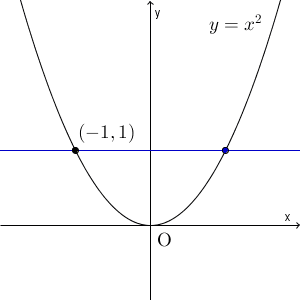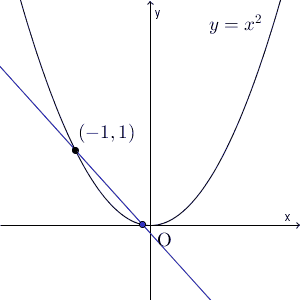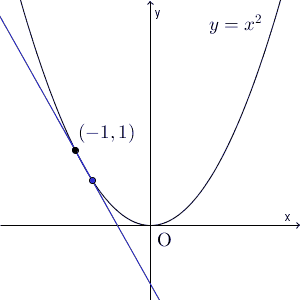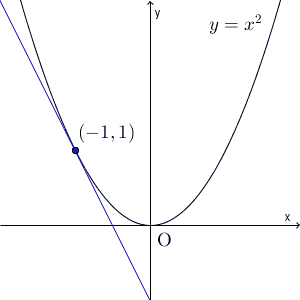
なんだか、2点を結んだ直線はある直線にすごく近づいているような気がしますね。

このとき、平均変化率がどのようになっているか、具体的に計算してみましょう。 x が $-1$ から b まで変化するとき、平均変化率は
\begin{eqnarray} \frac{b^2-1}{b-(-1)}=\frac{(b-1)(b+1)}{b+1}=b-1 \end{eqnarray}となります。なので、 b を $-1$ に近づけていけば、平均変化率は $-2$ に近づいていくことがわかります。これがマイナスであることと、「 $x=-1$ 付近では、 x が増えるたびに、 y が減ること」がうまく対応しているようです。

同じように計算すれば、 $x=1$ のときは、傾きが $2$ の直線に近づいていたことがわかり、これも「 $x=1$ 付近では、 x が増えるたびに、 y も増えること」とうまく対応しています。

さて、一番重要な $x=0$ のところを考えてみましょう。 $0⇒b$ と変化する場合、平均変化率は
\begin{eqnarray} \frac{b^2-0}{b-0}=b \end{eqnarray}となります。なので、 b を $0$ に近づけていけば、平均変化率は $0$ となります。これは「増えも減りもしない」こと、つまり、山や谷を表しているのではないか、と考えられますね。

こうした考えから、平均変化率の式で、区間をすごく狭くしていったときの値が重要だということが予想できます。この値のことを、微分係数(derivative) といいます。

ここでは、「すごく狭くする」とか「すごく近づく」などと書いて説明しましたが、数学ではこうしたことをスマートに書く方法があります。別の機会にその方法を紹介します（参考：【基本】極限値と微分係数）。微分係数をもう少しスッキリした形で書く方法も、そこで紹介します。