【基本】微分と関数の増減

ここでは、微分を用いて、関数の増減について考えていきます。ここで出てくる関数は、整式を想定しています。

導関数の復習

微分する、もしくは、導関数を求める、ということがどういうことだったかをもう一度振り返っておきましょう。

ある関数 $f(x)$ の導関数とは、各 $a$ に対して、 $x=a$ での関数 $f(x)$ の微分係数を対応させる関数のことでした（参考：【基本】導関数）。この微分係数は、次の式で求めることができます。\[ \lim_{h\to 0} \frac{f(a+h)-f(a)}{h} \]定義通りの式です。各 $a$ に上の極限値を対応させる関数を導関数というのでした。

ただ、整式の場合は、上の極限値を毎回計算しなくても、もっと簡単に導関数を求めることができます。 $x^n$ を微分すると $nx^{n-1}$ となるので、これを利用すればいいんでしたね（参考：【基本】整式の導関数）。 $x^3$ の導関数は $3x^2$, $x^2$ なら $2x$, $x$ なら $1$ となり、定数の導関数は $0$ となるのでした。

さらに、【基本】微分と接線の方程式で見たように、微分の考えを使って、接線についても考えるようになりました。ここでいう接線とは、関数上の2点 $(a,f(a))$, $(a+h,f(a+h))$ をつなぐ直線を考え、その2点間の距離を縮めていったとき（ $h\to 0$ ）に近づく直線、と考えるのでしたね。この直線の傾きが、その点での微分係数と一致するのでした。

次の図は、 $y=2x^3-x$ の $x=-1$ での接線に関するものです。

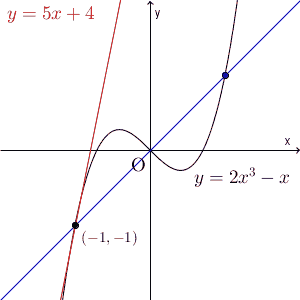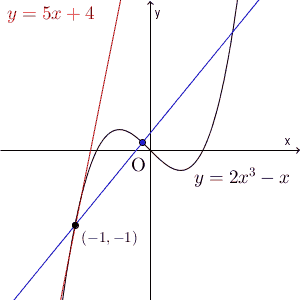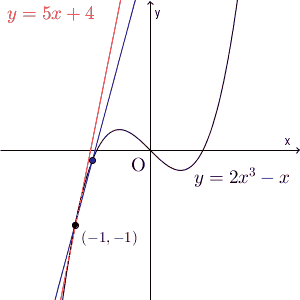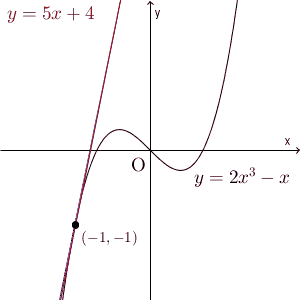
これを逆に考えれば、接点付近は、もとの関数と接線は同じような変化をする、ととらえることができます。 $(a,f(a))$, $(a+h,f(a+h))$ を結んだ直線が接線に近づいていくのだから、接点付近であれば、この直線と接線はだいたい似ている変化になっているはずです。

「変化の仕方が似ている」ことがわかっても、「だからどうした」という気がするかもしれませんが、これはとても重要です。関数のグラフの概形をかくために十分な情報が得られるからです。

よく知っている関数を使って、もう少し詳しく見ていきましょう。

微分と関数の増減

二次関数 $y=x^2$ について考えましょう。このグラフは、よく知っているように、下のようになります。

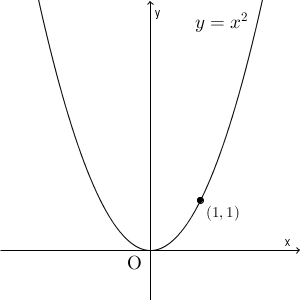
$y=x^2$ の導関数は、 $y'=2x$ です。なので、例えば、 $x=1$ のときは、 $y'=2$ です。つまり、ここでの接線の傾きは $2$ です。

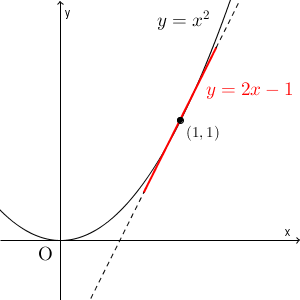
先ほど考えたように、 $x=1$ 付近ではこの接線と同じように、「だんだん増えていく」変化となりますが、 $x=1$ と離れてくると、関数のグラフと接線は離れていきます。しかし、また新しく接線の傾きを考えてみましょう。例えば、 $x=1.2$ なら $y'=2.4$ で、 $x=0.8$ なら $y'=1.6$ です。

関数の変化を見ると、傾きの大小ではなく、傾きが正であることが大事であることがわかります。接線の傾きが正であれば、その近辺では接線と同じように「 x が増えれば y も増えていくのだろう」と考えられます。さらに、そのような「接線の傾きが正」の部分が続けば、その間は「 x が増えれば y も増えていく」ことが言えることになります。

つまり、ある区間で導関数が正なら、（元の関数と動きが似ている）接線の傾きが正ということなので、その区間では関数は「だんだん増えていく」ことが言えます。

逆に、 $x=-1$ のときは、 $y'=-2$ となり、負となります。この近辺では、だんだん減っていくことがわかります。ただ、導関数は $y'=2x$ なので、 $x\lt 0$ の間はずっと導関数は負の値をとります。そのため、 $x=-1$ の近辺でまた接線を考えると、やはりその付近でも「だんだん減る」ことがわかり、またその近辺で接線を考えると…と繰り返していけば、 $x\lt 0$ の間は「 x が増えれば y は減っていく」ことが言えます。

$y=x^2$ のグラフを知っているから当たり前な気がしますが、ここで重要なのは、導関数の符号を調べるだけで、どの範囲で増加してどの範囲で減少するかがわかる、ということなんですね。これが分かれば、減少から増加に転じるところが谷底になる、というようにグラフの概形が分かるようになります。

なお、上で出てきた、「 x が増えれば y も増えていく」などと言う言葉は、数学の世界では、単調(monotonically) という言葉を使って次のように表現します。

例えば、 $y=x^2$ は、 $x\lt 0$ で単調に減少し、 $x\gt 0$ で単調に増加する、といいます。「単調に増加」というのは、減るところがなくて、ずっと増え続ける、ということです。

ここで見てきたことをまとめると、次のようになります。

おわりに

ここでは、導関数の符号を調べれば、関数の増減がわかる、ということを見てきました。各点で、関数の動きは接線の動きと似ているため、導関数の符号を見れば、増え続けるか減り続けるか、ということがわかります。

これを利用してグラフをどのようにかいていくか、その具体的な方法については今後さらに深く見ていくことにしましょう。