【基本】絶対値のついた関数の定積分

🕒 2017/11/30 🔄 2023/05/01

ここでは、絶対値を含んだ関数の定積分を求める方法を見ていきます。面積との関連についても考えていきます。

📘 目次

絶対値のついた関数の定積分

まずは、絶対値の復習をしておきましょう。「 x の絶対値」というのは、数直線上での、実数 x と原点 $0$ との距離のことです。 $|3|=|-3|=3$ などとなります。たいていの場合、「マイナスをとるだけ」ですが、そうでないケースもあるので注意しましょう。例えば、 $|1-\sqrt{2}|$ は $\sqrt{2}-1$ と一致します。これらの話は、【基本】絶対値で詳しく書いています。

この「絶対値」のついた関数の定積分を求めてみましょう。例えば、次のような定積分を考えます。\[ \int_0^2 |x^2-1| dx \]この定積分を面積で表せば、下の図の色のついた部分の面積にあたります。

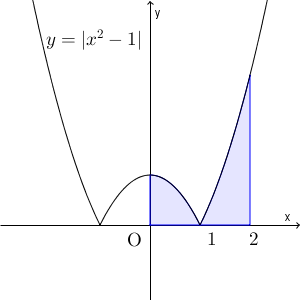
絶対値の計算は、まず絶対値を外せないかを考えるのが基本です。絶対値を外さないことには、これ以上計算ができません。

しかし、今の場合、単純に外すことはできません。というのも、 $x^2-1$ は正になったり負になったりするからです。 $0\leqq x \leqq 1$ の場合は負、 $1\leqq x \leqq 2$ の場合は正となります。区間によって、正負の状況が異なります。

そのため、区間を分けて考えることになります。【基本】定積分の性質#積分区間に関する定積分の性質で見たように、区間を分けて、次のように計算することができます。
\begin{eqnarray} & & \int_0^2 |x^2-1| dx \\[5px] &=& \int_0^1 |x^2-1| dx+\int_1^2 |x^2-1| dx \\[5px] &=& \int_0^1 (1-x^2) dx+\int_1^2 (x^2-1) dx \\[5px] &=& \left[ x-\frac{x^3}{3} \right]_0^1 +\left[ \frac{x^3}{3}-x \right]_1^2 \\[5pt] &=& \left(\frac{2}{3}-0\right) +\left(\frac{2}{3}+\frac{2}{3}\right) \\[5pt] &=& 2 \end{eqnarray}となります。

絶対値のついた関数の定積分は、絶対値を外せるように積分区間を分け、それから絶対値を外す、というのがポイントです。その後は、普通の定積分の計算です。

絶対値のついた関数の定積分と面積

絶対値のついた関数の定積分について、もう少し考えてみましょう。

先ほど見た計算は、【基本】曲線とx軸の間の面積と積分#放物線とx軸の間の面積（x軸をまたぐ）とすごく似ています。このリンク先の計算では、 $y=x^2-1$ と $x=0$, $x=2$, x 軸で囲まれた部分の面積の合計を求めていました。

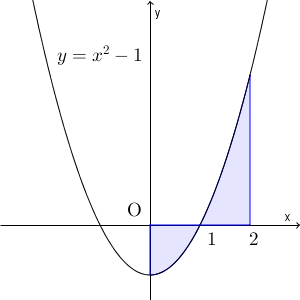
これは、 $y=x^2-1$ と $y=0$ (x 軸)との差を積分していることになります。 $y=x^2-1$ の方が上なら、 $(x^2-1)-0$ を積分し、 $y=x^2-1$ の方が下なら、 $0-(x^2-1)$ を積分することになります。これをよく見れば、 $|(x^2-1)-0|$ を積分していることと一致しています。

【基本】2曲線間の面積と積分で見た通り、 $a\leqq x \leqq b$ の範囲で、 $f(x)\geqq g(x)$ なら、 $y=f(x)$, $y=g(x)$, $x=a$, $x=b$ で囲まれた部分の面積は\[ \int_a^b (f(x)-g(x))dx \]となります。しかし、 $f(x)\geqq g(x)$ という条件がなくても、「上から下を引いて積分する」ということは、絶対値を用いて、\[ \int_a^b |f(x)-g(x)|dx \]と書くこともできます。こう書けば、 $f(x)$, $g(x)$ の大小関係によらず、「上から下を引いて積分する」ことになります。

ただ、この書き方は、表記が簡潔になるというだけで、計算するときには、やはり、積分区間を分けて積分記号を外して、という手順をとることになります。残念ながら、計算が楽になる、というわけではありません。