【基本】2つの円の共有点（中心間の距離に注目）

ここでは、2つの円の共有点の個数について見ていきます。中心間の距離に注目して考えていきます。

2つの円の共有点の個数

円と直線の共有点を考える場合、座標を求めたいなら、【基本】円と直線の共有点（二次方程式に注目）で見たように、2つの方程式から解を求めることになります。一方、共有点の個数だけが分かればいい場合は、【基本】円と直線の共有点（中心からの距離に注目）についてだけ、考えればOKでしたね。

2つの円の共有点の場合も同様です。共有点の座標を求めたいなら、【基本】2つの円の共有点（方程式に注目）で見たように、2つの方程式から解を求めることになりますが、共有点の個数だけならもっと省略できます。

円と直線の場合と同じように、2つの円の中心の距離で考えてみましょう。（参考：【基本】2つの円と共通接線）

半径が $r_1,r_2$ の2つの円があるとします。 $r_1 \gt r_2$ としておきます。また、中心間の距離を $d$ とおきます。

このとき、 $d,r_1,r_2$ の関係と、共有点の個数について考えてみましょう。

まず、2つの円が離れているときは、共有点はないですね。

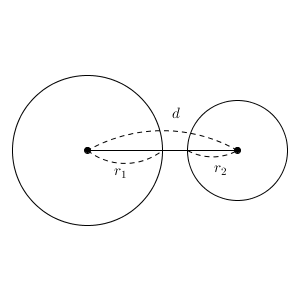
しかし、距離が縮まってくると、いつかは共有点を持つようになります。共有点を持つ瞬間をかいたものが次の図となります。

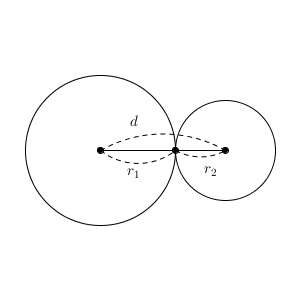
中心間の距離が半径の和になるとき、共有点が1点になります。このとき、2つの円は「接する」といいます。また、互いの円の外側で接しているので、「外接する」といいます。

図より、上の2つのケースは、それぞれ $d\gt r_1+r_2$, $d=r_1+r_2$ という条件で書けることがわかります。そして、中心間の距離がもっと縮まれば、今度は共有点が2点になります。

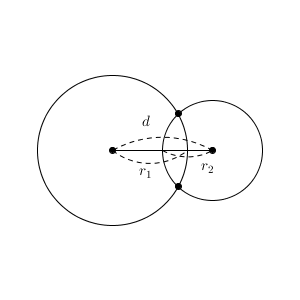
さらに距離が縮んでいくと、再び共有点が1点になります。

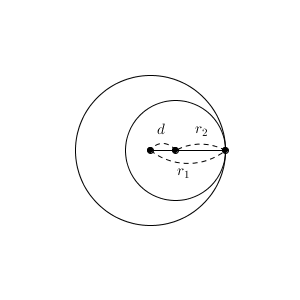
このときも、「接する」と言いますが、上の「外接」とは違うため、このケースは「内接する」といって、区別します。

そして、もっと縮まれば、完全に含まれて再び共有点がなくなるときが生まれます。

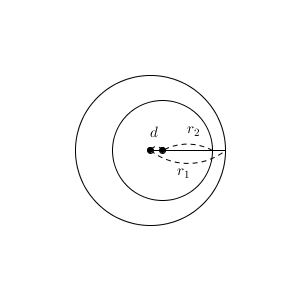
2つの円が内接するとき、中心間の距離が半径の差になるので $d=r_1-r_2$ となります。これが、共有点が2つか1つかなしか、の境目になります。

まとめると、次のようになります。

例えば、【基本】2つの円の共有点（方程式に注目）で見た例で考えましょう。

2つの円 $x^2+y^2=25$, $x^2-14x+y^2-2y+25=0$ の共有点の個数を考えてみます。1つ目の円は、原点が中心で半径が $5$ ですね。2つ目の円は
\begin{eqnarray} x^2-14x+y^2-2y+25 &=& 0 \\[5pt] (x-7)^2-49+(y-1)^2-1 &=& -25 \\[5pt] (x-7)^2+(y-1)^2 &=& 25 \\[5pt] \end{eqnarray}なので、中心が $(7,1)$ で、半径が $5$ の円です。

中心間の距離は $\sqrt{7^2+1^2}=5\sqrt{2}$ であり、\[ 5-5 \lt 5\sqrt{2} \lt 5+5 \]なので、共有点は2つだとわかります。半径が同じ円の場合は、上のまとめには含まれていませんが、同じように考えれば、5つのうち上の3つは同じように成り立つことは、図をかけばすぐにわかるでしょう。

共通接線

ところで、上のまとめでは、共有点の個数が「0⇒1⇒2⇒1⇒0」となっていて、きれいに分かれている感じがしませんよね。0と1が2回出てきて、かぶっています。この5つのケースにきれいに対応するものがあれば、分けやすくなります。

実は、うまく対応するものがあります。2つの円の両方に接する接線の数に注目します。このような接線のことを共通接線といいます。それぞれのケースで、共通接線が何本引けるか考えてみましょう。

まず、片方が片方に含まれている場合、共通接線は引けませんね。しかし、内接する場合は、1本引けます。

共有点が2点のときは、共通接線は2本引けます。

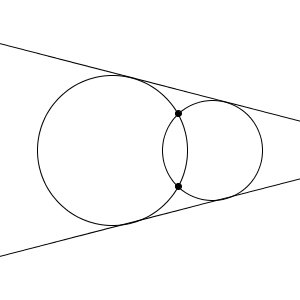
外接する場合は3本引けます。

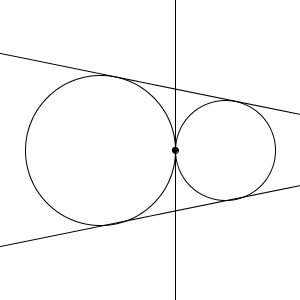
順番にいくと、さらに離れている場合は4本引けるはずです。少し思いつきにくいですが、次のようになりますね。

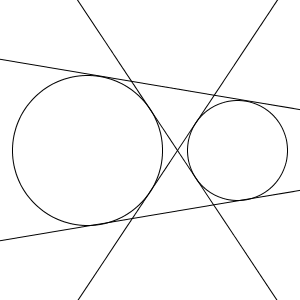
共有点の個数は、中心間の距離によって変わりました。そして、その切り替わる境目は、上で見たように共通接線の数の境目に対応しているのですね。

2つの円の位置関係を言うときに、共有点の個数ではなく、共通接線の数が使われることもあるので、半径と中心間のと距離とどういうふうに対応しているか、絵で見て理解しておきましょう。

おわりに

ここでは、2つの円の共有点の個数について考えました。半径と中心間との距離を考えればいいのでしたね。共通接線との関係もよく見ておきましょう。