【基本】三角比と三角形の面積

🕒 2016/10/18 🔄 2026/07/31

ここでは、 $\sin$ を使って三角形の面積を表す方法を見ていきます。

なお、辺 $\mathrm{AB}$, $\mathrm{BC}$, $\mathrm{CA}$ の長さを、それぞれ、 $c,a,b$ と書き、角 $\angle \mathrm{ CAB }$, $\angle \mathrm{ ABC }$, $\angle \mathrm{ BCA }$ の大きさを、それぞれ、 $A,B,C$ と書くことにします。

sinを用いた三角形の面積

三角形の面積は、「底辺×高さ÷２」で求められることは小学校のときに習いましたね。実は三角形の面積というのは、高校数学でもいろいろな形でよく出てきます。ここでは三角比を使った表し方を見ていきます。

$\triangle \mathrm{ ABC }$ について、 C から AB に垂線をおろし、その足を H とします。すると、この三角形の面積 S は\[ \frac{1}{2}\mathrm{ AB }\cdot \mathrm{ CH } \]と書くことができます。

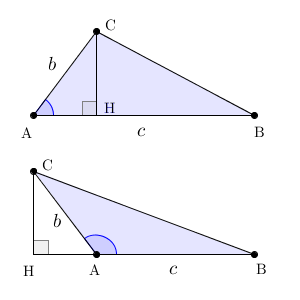
$\triangle \mathrm{ ACH }$ に注目して、この CH を三角比を用いて書いてみます。 A が鋭角のときは $b\sin A$ と書けます。直角のときは、 $\mathrm{ CH }=b$ であり、 $\sin A=1$ なので、このときも $b\sin A$ と書けます。鈍角のときは、 $b\sin (180^{\circ}-A)$ ですが、補角の公式から、これは $b\sin A$ と等しくなります。つまり、どの場合も、 $\mathrm{ CH }=b\sin A$ と書けることがわかります。

このことから、\[ S=\frac{1}{2}\mathrm{ AB }\cdot \mathrm{ CH }=\frac{1}{2}bc\sin A \]と表せることがわかります。同様にすれば、次のことがわかります。

三角形の面積（三角比バージョン）

$\triangle \mathrm{ ABC }$ の面積 S について、次が成り立つ。
\[ S=\frac{1}{2}bc\sin A =\frac{1}{2}ca\sin B =\frac{1}{2}ab\sin C \]

どの式でも、「2辺とその間の角」を使っています。

例題

$a=2\sqrt{2}$, $b=\sqrt{6}$, $C=30^{\circ}$ のとき、 $\triangle \mathrm{ ABC }$ の面積を求めなさい。

先ほどの公式にそのまま代入すれば求められます。
\begin{eqnarray} \frac{1}{2}ab\sin C &=& \frac{1}{2}\times 2\sqrt{2}\times\sqrt{6}\times\frac{1}{2} \\[5pt] &=& \sqrt{3} \\[5pt] \end{eqnarray}となります。