共通テスト 数学I・数学A 2017年度プレテスト 第5問 解説

2017年11月に実施された、大学入試共通テスト導入に向けたプレテストの問題です。元の資料をできる限り再現していますが、一部でレイアウトが変わっています。画像は、大学入試センターのサイトから取得しています。

【選択問題】(第3問～第5問から2問選択)

問題編

問題

　n を $3$ 以上の整数とする。紙に正方形のマスが縦横とも $(n-1)$ 個ずつ並んだマス目を書く。その $(n-1)^2$ 個のマスに、以下のルールに従って数字を一つずつ書き込んだものを「方盤」と呼ぶことにする。なお、横の並びを「行」、縦の並びを「列」という。

　ルール： 上から k 行目、左から $\ell$ 列目のマスに、k と $\ell$ の積を n で割った余りを記入する。

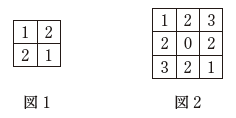
　$n=3$, $n=4$ のとき、方盤はそれぞれ下の図１, 図２のようになる。

　例えば、図２において、上から2行目、左から3列目には、 $2\times 3=6$ を $4$ で割った余りである $2$ が書かれている。このとき、次の問いに答えよ。

(1)　$n=8$ のとき、下の図３の方盤の A に当てはまる数を答えよ。 $\myBox{ア}$

　また、図３の方盤の上から５行目に並ぶ数のうち、 $1$ が書かれているのは左から何列目であるかを答えよ。左から $\myBox{イ}$ 列目

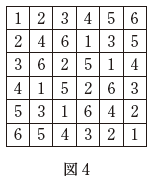
(2)　$n=7$ のとき、下の図４のように、方盤のいずれのマスにも $0$ が現れない。

　このように、方盤のいずれのマスにも $0$ が現れないための、n に関する必要十分条件を、次の 0～5 のうちから一つ選べ。 $\myBox{ウ}$

　0: $n$ が奇数であること。
　1: $n$ が $4$ で割って $3$ 余る整数であること。

　2: $n$ が $2$ の倍数でも $5$ の倍数でもない整数であること。
　3: $n$ が素数であること。

　4: $n$ が素数ではないこと。
　5: $n-1$ と $n$ が互いに素であること。

(3)　n の値がもっと大きい場合を考えよう。方盤においてどの数字がどのマスにあるかは、整数の性質を用いると簡単に求めることができる。

　$n=56$ のとき、方盤の上から $27$ 行目に並ぶ数のうち、 $1$ は左から何列目にあるかを考えよう。

(i)　方盤の上から $27$ 行目、左から $\ell$ 列目の数が $1$ であるとする（ただし、$1\leqq \ell \leqq 55$ ）。 $\ell$ を求めるためにはどのようにすれば良いか。正しいものを、次の 0～3 のうちから一つ選べ。 $\myBox{エ}$

　0: １次不定方程式 $27\ell-56m=1$ の整数解のうち、 $1\leqq \ell \leqq 55$ を満たすものを求める。

　1: １次不定方程式 $27\ell-56m=-1$ の整数解のうち、 $1\leqq \ell \leqq 55$ を満たすものを求める。

　2: １次不定方程式 $56\ell-27m=1$ の整数解のうち、 $1\leqq \ell \leqq 55$ を満たすものを求める。

　3: １次不定方程式 $56\ell-27m=-1$ の整数解のうち、 $1\leqq \ell \leqq 55$ を満たすものを求める。

(ii)　(i)で選んだ方法により、方盤の上から $27$ 行目に並ぶ数のうち、 $1$ は左から何列目にあるかを求めよ。左から $\myBox{オカ}$ 列目

(4)　$n=56$ のとき、方盤の各行にそれぞれ何個の $0$ があるか考えよう。

(i)　方盤の上から $24$ 行目には $0$ が何個あるか考える。

　左から $\ell$ 列目が $0$ であるための必要十分条件は、 $24\ell$ が $56$ の倍数であること、すなわち、 $\ell$ が $\myBox{キ}$ の倍数であることである。したがって、上から $24$ 行目には $0$ が $\myBox{ク}$ 個ある。

(ii)　上から $1$ 行目から $55$ 行目までのうち、 $0$ の個数が最も多いのは上から何行目であるか答えよ。上から $\myBox{ケコ}$ 行目

(5)　$n=56$ のときの方盤について、正しいものを、次の 0～5 のうちからすべて選べ。 $\myBox{サ}$

　0: 上から $5$ 行目には $0$ がある。
　1: 上から $6$ 行目には $0$ がある。

　2: 上から $9$ 行目には $1$ がある。
　3: 上から $10$ 行目には $1$ がある。

　4: 上から $15$ 行目には $7$ がある。
　5: 上から $21$ 行目には $7$ がある。

考え方

方盤というものを使っていますが、整数の性質に関する問題です。倍数・約数や余り、不定一次方程式の整数解を扱っています。設定を理解しながら、整数のどんな性質を利用すればいいのかを考えていきましょう。

(5)はそれまでの問題で考えたことを利用して取り組みましょう。正しいものをすべて選ばないといけないので、各選択肢について1つ1つ考えないといけません。選択肢はどれも似た形をしていますが、選択肢によって考えるポイントや使う性質はまったく異なります。特に、4と5をどう考えるかが難しいです。

2017年11月に実施された、大学入試共通テスト導入に向けたプレテストの問題です。元の資料をできる限り再現していますが、一部でレイアウトが変わっています。画像は、大学入試センターのサイトから取得しています。

【選択問題】(第3問～第5問から2問選択)

解答編

問題

　n を $3$ 以上の整数とする。紙に正方形のマスが縦横とも $(n-1)$ 個ずつ並んだマス目を書く。その $(n-1)^2$ 個のマスに、以下のルールに従って数字を一つずつ書き込んだものを「方盤」と呼ぶことにする。なお、横の並びを「行」、縦の並びを「列」という。

　ルール： 上から k 行目、左から $\ell$ 列目のマスに、k と $\ell$ の積を n で割った余りを記入する。

　$n=3$, $n=4$ のとき、方盤はそれぞれ下の図１, 図２のようになる。

　例えば、図２において、上から2行目、左から3列目には、 $2\times 3=6$ を $4$ で割った余りである $2$ が書かれている。このとき、次の問いに答えよ。

(1)　$n=8$ のとき、下の図３の方盤の A に当てはまる数を答えよ。 $\myBox{ア}$

解説

書いてあるルールがきちんと理解できているかを確認するための問題です。ルール通りに求めればＯＫです。

図３のA は、上から6行目、左から3列目なので、 $6\times 3=18$ を $n=8$ で割った余り $2$ が入ります。

解答

ア：2

解答編 つづき

問題

　また、図３の方盤の上から５行目に並ぶ数のうち、 $1$ が書かれているのは左から何列目であるかを答えよ。左から $\myBox{イ}$ 列目

解説

5行目には、5の倍数を8で割った余りが並ぶことがわかります。順番に考えていけば、 $5\times 5=25$ を $n=8$ で割ると余りが $1$ となるので、5列目であることがわかります。

解答

イ：5

解答編 つづき

問題

(2)　$n=7$ のとき、下の図４のように、方盤のいずれのマスにも $0$ が現れない。

　このように、方盤のいずれのマスにも $0$ が現れないための、n に関する必要十分条件を、次の 0～5 のうちから一つ選べ。 $\myBox{ウ}$

　0: $n$ が奇数であること。
　1: $n$ が $4$ で割って $3$ 余る整数であること。

　2: $n$ が $2$ の倍数でも $5$ の倍数でもない整数であること。
　3: $n$ が素数であること。

　4: $n$ が素数ではないこと。
　5: $n-1$ と $n$ が互いに素であること。

解説

マスに $0$ が現れるときとはどういうときかを考えましょう。

k 行目、 $\ell$ 列目のマスが $0$ だったとすると、 $k\ell$ が n で割り切れるということですね。つまり、 $n$ より小さい自然数の積で $n$ の倍数を作れるときです。

ですので、 $0$ が現れないということは、 $n$ より小さい2つの自然数をどのように掛けても、 $n$ の倍数が作れないということなので、 $n$ を作ることもできないので、 $n$ が素数のときであることがわかります。逆に、素数なら、マスに $0$ が現れないこともわかりますね。

ちなみに、図１と図４を見れば、 $n=3,7$ のときはマスに $0$ が現れないことがわかります。さらに、 $n=2$ のときは、 $1$ しか現れないので、この場合も $0$ は現れません。選択肢の中で、 $n=2,3,7$ を含むものは、「n が素数」と「 $n$ と $n-1$ が互いに素」しかありません。「 $n$ と $n-1$ が互いに素」は $n=4$ のときも含んでしまうのでダメです。このことからも、「 $n$ が素数」が答えであることがわかります。

解答

ウ：3

解答編 つづき

問題

(3)　n の値がもっと大きい場合を考えよう。方盤においてどの数字がどのマスにあるかは、整数の性質を用いると簡単に求めることができる。

　$n=56$ のとき、方盤の上から $27$ 行目に並ぶ数のうち、 $1$ は左から何列目にあるかを考えよう。

(i)　方盤の上から $27$ 行目、左から $\ell$ 列目の数が $1$ であるとする（ただし、$1\leqq \ell \leqq 55$ ）。 $\ell$ を求めるためにはどのようにすれば良いか。正しいものを、次の 0～3 のうちから一つ選べ。 $\myBox{エ}$

　0: １次不定方程式 $27\ell-56m=1$ の整数解のうち、 $1\leqq \ell \leqq 55$ を満たすものを求める。

　1: １次不定方程式 $27\ell-56m=-1$ の整数解のうち、 $1\leqq \ell \leqq 55$ を満たすものを求める。

　2: １次不定方程式 $56\ell-27m=1$ の整数解のうち、 $1\leqq \ell \leqq 55$ を満たすものを求める。

　3: １次不定方程式 $56\ell-27m=-1$ の整数解のうち、 $1\leqq \ell \leqq 55$ を満たすものを求める。

(ii)　(i)で選んだ方法により、方盤の上から $27$ 行目に並ぶ数のうち、 $1$ は左から何列目にあるかを求めよ。左から $\myBox{オカ}$ 列目

解説

$27$ 行目、 $\ell$ 列目に入る数は、 $27\ell$ を $n=56$ で割った余りです。これが $1$ になるということは、ある整数 m を用いて\[ 27\ell=56m+1 \]と書けるということです。なので、\[ 27\ell-56m=1 \]が成り立つような $\ell$ を見つければいいことがわかります。

この式は、
\begin{eqnarray} 27\ell -56m &=& 1 \\[5pt] 27\ell -(27\times 2+2)m &=& 1 \\[5pt] 27(\ell-2m) -2m &=& 1 \\[5pt] \end{eqnarray}と変形できます。これを満たすものはたくさんありますが、すぐに思いつくものとして、 $m=13,\ell-2m=1$ の組合せがあります。このとき、たまたま $\ell=27$ となり、条件を満たすので、これが答えとなります。

一般的には、\[ 27\times 1 -2\times 13=1 \]を先ほどの式から引いて
\begin{eqnarray} 27(\ell-2m-1) -2(m-13) &=& 0 \\[5pt] 27(\ell-2m-1) &=& 2(m-13) \\[5pt] \end{eqnarray}と変形します。 $2,27$ が互いに素だから、\[ m-13=27k, \ell-2m-1=2k \]と書ける（k は整数）ことがわかります。 $m=27k+13$ だから \begin{eqnarray} \ell-2m-1 &=& 2k \\[5pt] \ell-2(27k+13)-1 &=& 2k \\[5pt] \ell &=& 2k+2(27k+13)+1 \\[5pt] \ell &=& 56k+27 \\[5pt] \end{eqnarray}と導きます。このうち、条件を満たすようなものを探せば、 $k=0$ のときの $\ell=27$ だと求められます。

解答

エ：0
オカ：27

参考

【応用】不定一次方程式 係数が大きい場合

解答編 つづき

問題

(4)　$n=56$ のとき、方盤の各行にそれぞれ何個の $0$ があるか考えよう。

(i)　方盤の上から $24$ 行目には $0$ が何個あるか考える。

　左から $\ell$ 列目が $0$ であるための必要十分条件は、 $24\ell$ が $56$ の倍数であること、すなわち、 $\ell$ が $\myBox{キ}$ の倍数であることである。したがって、上から $24$ 行目には $0$ が $\myBox{ク}$ 個ある。

(ii)　上から $1$ 行目から $55$ 行目までのうち、 $0$ の個数が最も多いのは上から何行目であるか答えよ。上から $\myBox{ケコ}$ 行目

解説

$24\ell$ が $56$ の倍数ということは、\[ 24\ell =56m \]となる整数 m があるということですね。これは\[ 3\ell=7m \]となる整数 m があるということです。両辺は $7$ の倍数なので、 $\ell$ は $7$ の倍数でないといけません。逆に、 $7$ の倍数であれば、 $24\ell$ は $56$ の倍数となります。

$55$ 以下の自然数のうち、 $7$ の倍数は $7$ 個あるので、 $24$ 行目には $0$ が $7$ 個並ぶことがわかります。

同様に考えれば、 $0$ の個数が最も多くなるのは、偶数番目の列に $0$ が並ぶときです。こうなるのは、28行目ですね。「 $28\ell$ が $56$ の倍数」と「 $\ell$ が2の倍数」が同値だからです。これが(ii)の答えです。

解答

キ：7
ク：7
ケコ：28

解答編 つづき

問題

(5)　$n=56$ のときの方盤について、正しいものを、次の 0～5 のうちからすべて選べ。 $\myBox{サ}$

　0: 上から $5$ 行目には $0$ がある。
　1: 上から $6$ 行目には $0$ がある。

　2: 上から $9$ 行目には $1$ がある。
　3: 上から $10$ 行目には $1$ がある。

　4: 上から $15$ 行目には $7$ がある。
　5: 上から $21$ 行目には $7$ がある。

解説

1つ1つ見ていきましょう。

上から5行目には、5の倍数を56で割った余りが並びます。5と56は互いに素なので、マスに $0$ が現れることはありません。

上から6行目には、6の倍数を56で割った余りが並びます。28行目は、 $3\times 2\times 28$ を56で割った余りが入ります。割り切れるので、 $0$ が入ります。

上から9行目には、9の倍数を56で割った余りが並びます。もし a 列目と b 列目のマスの値が同じなら、 $9a-9b$ は56で割り切れることになってしまいますが、9と56は互いに素なので、こんなことは起こりません。よって、余りはすべて異なります。また、割り切れることもないので、1列目から55列目までの中に、1から55が1回ずつ現れます。よって、1があることがわかります。

上から10行目には、10の倍数を56で割った余りが並びます。余りは偶数になるので、1になることはありません。

上から15行目には、15の倍数を56で割った余りが並びます。これも9行目のときと同様に、「15と56が互いに素」なので、15の倍数を56で割った余りは、すべて異なります。1から55が1回ずつ現れるので、7があることもわかります。

上から21行目には、21の倍数を56で割った余りが並びます。これは「3の倍数を8で割った余り、を7倍したもの」です。3と8は互いに素なので、1列目から7列目までを見ると、 $7\times 1$ から $7\times 7$ が1回ずつ現れます。よって、7は現れます。実際、 $21\times 3=56+7$ なので、3列目に表れますね。

「余りが0になることがない」と「互いに素」の関係、また、「互いに素」と「余りが異なる」の関係は有名なので、選択肢0から選択肢4までは正しく判断できる人は多いと思いますが、最後の5は見方を変えないといけないので、少し難易度が高いですね。

解答

サ：1,2,4,5