共通テスト 数学I・数学A 2017年度プレテスト 第2問 [1] 解説

2017年11月に実施された、大学入試共通テスト導入に向けたプレテストの問題です。元の資料をできる限り再現していますが、一部でレイアウトが変わっています。画像は、大学入試センターのサイトから取得しています。

【必答問題】

問題編

問題

　◯◯高校の生徒会では、文化祭でＴシャツを販売し、その利益をボランティア団体に寄付する企画を考えている。生徒会執行部では、できるだけ利益が多くなる価格を決定するために、次のような手順で考えることにした。

【価格決定の手順】
(i) アンケート調査の実施
　200人の生徒に、「Ｔシャツ１枚の価格がいくらまでであればＴシャツを購入してもよいと思うか」について尋ね、500円、1000円、1500円、2000円の四つの金額から一つを選んでもらう。
(ii) 業者の選定
　無地のＴシャツ代とプリント代を合わせた「製作費用」が最も安い業者を選ぶ。
(iii) Ｔシャツ１枚の価格の決定
　価格は「製作費用」と「見込まれる販売数」をもとに決めるが、販売時に釣り銭の処理で手間取らないよう50の倍数の金額とする。

　下の表１は、アンケート調査の結果である。生徒会執行部では、例えば、価格が1000円のときには1500円や2000円と回答した生徒も１枚購入すると考えて、それぞれの価格に対し、その価格以上の金額を回答した生徒の人数を「累積人数」として表示した。

表１

Ｔシャツ1枚の価格（円）	人数（人）	累積人数（人）
2000	50	50
1500	43	93
1000	61	154
500	46	200

　このとき、次の問いに答えよ。

(1) 売上額は
　（売上額）＝（Ｔシャツ１枚の価格）×（販売数）
と表せるので、生徒会執行部では、アンケートに回答した200人の生徒について、調査結果をもとに、表１にない価格の場合についても販売数を予測することにした。そのために、Ｔシャツ１枚の価格を x 円、このときの販売数を y 枚とし、 x と y の関係を調べることにした。
　表１のＴシャツ１枚の価格と $\myBox{ア}$ の値の組を $(x,y)$ として座標平面上に表すと、その４点が直線に沿って分布しているように見えたので、この直線を、Ｔシャツ１枚の価格 x と販売数 y の関係を表すグラフとみなすことにした。
　このとき、 y は x の $\myBox{イ}$ であるので、売上額を $S(x)$ とおくと、 $S(x)$ は x の $\myBox{ウ}$ である。このように考えると、表１にない価格の場合についても売上額を予測することができる。

　$\myBox{ア}$, $\myBox{イ}$, $\myBox{ウ}$ に入るものとして最も適当なものを、次の 0～6 のうちから一つずつ選べ。ただし、同じものを繰り返し選んでもよい。

　0: 人数
　1: 累積人数
　2: 製作費用
　3: 比例
　4: 反比例
　5: １次関数
　6: ２次関数

　生徒会執行部が(1)で考えた直線は、表１を用いて座標平面上にとった４点のうち x の値が最小の点と最大の点を通る直線である。この直線を用いて、次の問いに答えよ。

(2) 売上額 $S(x)$ が最大になる x の値を求めよ。 $\myBox{エオカキ}$

(3) Ｔシャツ１枚当たりの「製作費用」が 400円の業者に120枚を依頼することにしたとき、利益が最大になるＴシャツ１枚の価格を求めよ。 $\myBox{クケコサ}$ 円

考え方

問題文が長いですが、2次関数の最大を求めているだけです。

問題文にある条件を、数式でどのように表現するかを考えながら解いていきましょう。計算自体は難しくありません。

(3)は(2)とどこが違うのかよく考えましょう。利益と売上額との関係にも着目して考えましょう。

2017年11月に実施された、大学入試共通テスト導入に向けたプレテストの問題です。元の資料をできる限り再現していますが、一部でレイアウトが変わっています。画像は、大学入試センターのサイトから取得しています。

【必答問題】

解答編

問題

　◯◯高校の生徒会では、文化祭でＴシャツを販売し、その利益をボランティア団体に寄付する企画を考えている。生徒会執行部では、できるだけ利益が多くなる価格を決定するために、次のような手順で考えることにした。

【価格決定の手順】
(i) アンケート調査の実施
　200人の生徒に、「Ｔシャツ１枚の価格がいくらまでであればＴシャツを購入してもよいと思うか」について尋ね、500円、1000円、1500円、2000円の四つの金額から一つを選んでもらう。
(ii) 業者の選定
　無地のＴシャツ代とプリント代を合わせた「製作費用」が最も安い業者を選ぶ。
(iii) Ｔシャツ１枚の価格の決定
　価格は「製作費用」と「見込まれる販売数」をもとに決めるが、販売時に釣り銭の処理で手間取らないよう50の倍数の金額とする。

　下の表１は、アンケート調査の結果である。生徒会執行部では、例えば、価格が1000円のときには1500円や2000円と回答した生徒も１枚購入すると考えて、それぞれの価格に対し、その価格以上の金額を回答した生徒の人数を「累積人数」として表示した。

表１

Ｔシャツ1枚の価格（円）	人数（人）	累積人数（人）
2000	50	50
1500	43	93
1000	61	154
500	46	200

　このとき、次の問いに答えよ。

(1) 売上額は
　（売上額）＝（Ｔシャツ１枚の価格）×（販売数）
と表せるので、生徒会執行部では、アンケートに回答した200人の生徒について、調査結果をもとに、表１にない価格の場合についても販売数を予測することにした。そのために、Ｔシャツ１枚の価格を x 円、このときの販売数を y 枚とし、 x と y の関係を調べることにした。
　表１のＴシャツ１枚の価格と $\myBox{ア}$ の値の組を $(x,y)$ として座標平面上に表すと、その４点が直線に沿って分布しているように見えたので、この直線を、Ｔシャツ１枚の価格 x と販売数 y の関係を表すグラフとみなすことにした。
　このとき、 y は x の $\myBox{イ}$ であるので、売上額を $S(x)$ とおくと、 $S(x)$ は x の $\myBox{ウ}$ である。このように考えると、表１にない価格の場合についても売上額を予測することができる。

　$\myBox{ア}$, $\myBox{イ}$, $\myBox{ウ}$ に入るものとして最も適当なものを、次の 0～6 のうちから一つずつ選べ。ただし、同じものを繰り返し選んでもよい。

　0: 人数
　1: 累積人数
　2: 製作費用
　3: 比例
　4: 反比例
　5: １次関数
　6: ２次関数

解説

なかなか問題が始まりませんが、状況を把握しないと答えられないので、よく読んで何をしたいのかを理解していくしかありません。

アについては、その後で、「Ｔシャツ１枚の価格 x と販売数 y の関係を表すグラフとみなす」と書いているので、「Ｔシャツ1枚の価格と販売数」を組としていることがわかります。空欄の後を見ないとわからないので、よく読む必要があります。

販売数とは買う人の人数です。問題文にある通り、「1500円と回答した人は1000円でも買う」などと考えるため、販売数は、累積人数のこととなります。

ちなみに、問題文には、「一人が複数のＴシャツを買うこと」は想定されていないようです。本来は2枚以上買ってもいいはずで、そうすると販売数と購入者数は異なるのですが、ここでは一人一枚まで、という前提が入ってしまっています。

さて、グラフが直線であることから、 x, y の関係は、比例か1次関数しかありません。どちらの値も0以上で、価格を上げると販売数は減ることから、比例はありえません。1次関数である、とわかります。

y は x の1次関数なので、\[ y=ax+b \]と書けます。売上額は、Ｔシャツ1枚の価格と販売数を掛けたものなので、 $xy$ ということですね。つまり、\[ S(x)=xy=ax^2+bx \]なので、2次関数となります。

解答

ア：1
イ：5
ウ：6

解答編 つづき

問題

　生徒会執行部が(1)で考えた直線は、表１を用いて座標平面上にとった４点のうち x の値が最小の点と最大の点を通る直線である。この直線を用いて、次の問いに答えよ。

(2) 売上額 $S(x)$ が最大になる x の値を求めよ。 $\myBox{エオカキ}$

解説

「x の値が最小の点と最大の点を通る直線で近似した」ことがわかるため、この直線を求めましょう。表１から、 x が最小のときは $500$ で、このときの y は $200$ です。また、 x が最大のときは $2000$ で、そのときの y は $50$ です。

これをもとに、 $y=ax+b$ の係数を求めましょう。 x を $1500$ 増やしたら、 y が $150$ 減るのだから、 $a=-\dfrac{1}{10}$ となります。 $x=500,y=200$ を代入すれば $b=250$ となります。よって、\[ y=-\frac{1}{10}x+250 \]となります。

これを用いて、売上高 $S(x)$ を計算すると
\begin{eqnarray} S(x) &=& xy \\[5pt] &=& -\frac{1}{10}x^2+250x \\[5pt] &=& -\frac{1}{10}(x^2-2500x) \\[5pt] &=& -\frac{1}{10}(x-1250)^2+\frac{1}{10}\times 1250^2 \\[5pt] \end{eqnarray}となります。

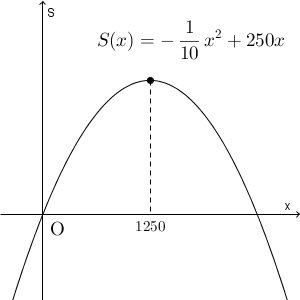
このグラフは上に凸なので、頂点で最大、つまり、 $x=1250$ のときに最大になることがわかります。

解答

エオカキ：1250

解答編 つづき

問題

(3) Ｔシャツ１枚当たりの「製作費用」が 400円の業者に120枚を依頼することにしたとき、利益が最大になるＴシャツ１枚の価格を求めよ。 $\myBox{クケコサ}$ 円

解説

製作費用が400円ということは、Ｔシャツ1枚の利益は $x-400$ だ、と思ってしまう人がいるかもしれませんが、そうではありません。120枚依頼することが決まっているので、1枚だけ売ろうが、120枚全部売ろうが、掛かるコストは\[ 400\times120 \]円となります。売上額からこの金額を引いたものが、利益です。コストは一定なので、利益が最大となるのは、売上額が最大となるときを考えればいいことがわかります。

(2)と異なるのは、Ｔシャツの枚数が限定されている点です。Ｔシャツは120枚しかありません。もし、(2)と同じように $x=1250$ とすると、 $y=125$ となってしまい、Ｔシャツが足りません。(2)と異なり、定義域が限定されていることに注意しましょう。

$y\leqq 120$ なので、\[ -\frac{1}{10}x+250 \leqq 120 \]となります。これを解くと
\begin{eqnarray} -\frac{1}{10}x+250 & \leqq & 120 \\[5pt] -\frac{1}{10}x & \leqq & -130 \\[5pt] x & \geqq & 1300 \\[5pt] \end{eqnarray}となります。

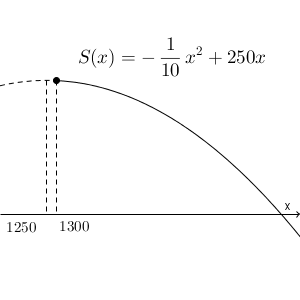
点 $(x,S(x))$ を集めてグラフをかくと、上に凸の放物線となります。範囲は頂点より右側の部分です。よって、売上が最大となるのは $x=1300$ のときであることがわかります。

問題文のはじめの方にある「価格決定の手順」では、「価格は50の倍数にする」と書いていますが、1300は50の倍数です。よって、価格は、1300円とすればいいことがわかります。

解答

クケコサ：1300