共通テスト 数学I・数学A 2017年度プレテスト 第1問 [1] 解説
2017年11月に実施された、大学入試共通テスト導入に向けたプレテストの問題です。元の資料をできる限り再現していますが、一部でレイアウトが変わっています。画像は、大学入試センターのサイトから取得しています。
【必答問題】
問題編
問題
数学の授業で、2次関数 $y= ax^2 + bx + c$ についてコンピュータのグラフ表示ソフトを用いて考察している。
このソフトでは、図1の画面上の $\myBox{A}$, $\myBox{B}$, $\myBox{C}$ にそれぞれ係数 a, b, c の値を入力すると、その値に応じたグラフが表示される。さらに、 $\myBox{A}$, $\myBox{B}$, $\myBox{C}$ それぞれの下にある・を左に動かすと係数の値が減少し、右に動かすと係数の値が増加するようになっており、値の変化に応じて2次関数のグラフが座標平面上を動く仕組みになっている。
また、座標平面は x 軸、y 軸によって四つの部分に分けられる。これらの各部分を「象限」といい、右の図のように、それぞれを「第1象限」「第2象限」「第3象限」「第4象限」という。ただし、座標軸上の点は、どの象限にも属さないものとする。
このとき、次の問いに答えよ。
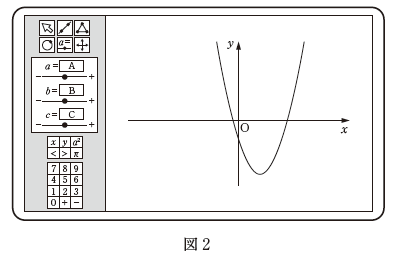
(1) はじめに、図1の画面のように、頂点が第3象限にあるグラフが表示された。このときの a, b, c の値の組合せとして最も適当なものを、次の 0~5 のうちから一つ選べ。 $\myBox{ア}$
a b c 0 $2$ $1$ $3$ 1 $2$ $-1$ $3$ 2 $-2$ $3$ $-3$ 3 $\frac{1}{2}$ $3$ $3$ 4 $\frac{1}{2}$ $-3$ $3$ 5 $-\frac{1}{2}$ $3$ $-3$ (2) 次に、a, b の値を(1)の値のまま変えずに、c の値だけを変化させた。このときの頂点の移動について正しく述べたものを、次の 0~3 のうちから一つ選べ。 $\myBox{イ}$
0: 最初の位置から移動しない。
1: x 軸方向に移動する。
2: y 軸方向に移動する。
3: 原点を中心として回転移動する。(3) また、b, c の値を(1)の値のまま変えずに、a の値だけをグラフが下に凸の状態を維持するように変化させた。このとき、頂点は、 $a=\dfrac{b^2}{4c}$ のときは $\myBox{ウ}$ にあり、 それ以外のときは $\myBox{エ}$ を移動した。 $\myBox{ウ}$, $\myBox{エ}$ に当てはまるものを、次の 0~8 のうちから一つずつ選べ。ただし、同じものを選んでもよい。
0: 原点
1: x 軸上
2: y 軸上
3: 第3象限のみ
4: 第1象限と第3象限
5: 第2象限と第3象限
6: 第3象限と第4象限
7: 第2象限と第3象限と第4象限
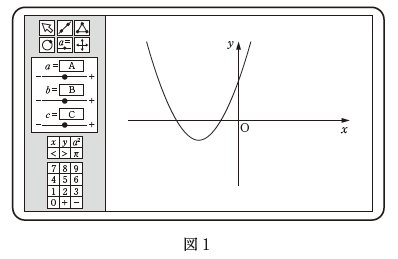
8: すべての象限(4) 最初の a, b, c の値を変更して、下の図2のようなグラフを表示させた。このとき、a, c の値をこのまま変えずに、b の値だけを変化させても、頂点は第1象限および第2象限には移動しなかった。
その理由を、頂点の y 座標についての不等式を用いて説明せよ。解答は、解答欄 $\myBox{(あ)}$ に記述せよ。
考え方
今までのセンター試験とは見た目が大きく変わっています。ただ、内容は、二次関数のグラフについてです。見た目に惑わされないようにしましょう。
1問目からわりとヘビーな内容です。計算するだけで得点できる問題はなく、一般的な状況を考える必要があり、数学が苦手な人にはどの問題も厳しいでしょう。(2)は(1)ができなくても解けますが、(1)でつまづいてしまうと戦意喪失してしまいそうです。
最後の記述も、どこまで書くことが求められているかはわかりにくいですが、条件で指定されている不等式と、その不等式が成り立つ理由を書けば十分でしょう。
文字での計算や、一般的な状況を考えるのが得意な人、本質的なことがわかっている人にとっては、複雑な計算が減った分、易しく感じられる人もいるかもしれません。一方で、数学が苦手だという人には、テクニック的な解法が使える箇所が少なく、とても難しく感じてしまうかもしれません。
2017年11月に実施された、大学入試共通テスト導入に向けたプレテストの問題です。元の資料をできる限り再現していますが、一部でレイアウトが変わっています。画像は、大学入試センターのサイトから取得しています。
【必答問題】
解答編
問題
数学の授業で、2次関数 $y= ax^2 + bx + c$ についてコンピュータのグラフ表示ソフトを用いて考察している。
このソフトでは、図1の画面上の $\myBox{A}$, $\myBox{B}$, $\myBox{C}$ にそれぞれ係数 a, b, c の値を入力すると、その値に応じたグラフが表示される。さらに、 $\myBox{A}$, $\myBox{B}$, $\myBox{C}$ それぞれの下にある・を左に動かすと係数の値が減少し、右に動かすと係数の値が増加するようになっており、値の変化に応じて2次関数のグラフが座標平面上を動く仕組みになっている。
また、座標平面は x 軸、y 軸によって四つの部分に分けられる。これらの各部分を「象限」といい、右の図のように、それぞれを「第1象限」「第2象限」「第3象限」「第4象限」という。ただし、座標軸上の点は、どの象限にも属さないものとする。
解説
今までのセンター試験と見比べると、すごく違和感のある出題になっています。ただ、よく見れば、二次関数のグラフをかいているだけです。見た目に騙されずに考えていきましょう。
なお、象限の話も、教科書で出てくる内容です。問題文で説明されていますが、説明されていなくてもどれがどこを指しているかは分かるようになっておきましょう。
参考
解答編 つづき
問題
このとき、次の問いに答えよ。
(1) はじめに、図1の画面のように、頂点が第3象限にあるグラフが表示された。このときの a, b, c の値の組合せとして最も適当なものを、次の 0~5 のうちから一つ選べ。 $\myBox{ア}$
a b c 0 $2$ $1$ $3$ 1 $2$ $-1$ $3$ 2 $-2$ $3$ $-3$ 3 $\frac{1}{2}$ $3$ $3$ 4 $\frac{1}{2}$ $-3$ $3$ 5 $-\frac{1}{2}$ $3$ $-3$
解説
図1を見直しておきましょう。
このグラフから、係数としてありえるものを考えていきます。
まず、下に凸なので、 a は正であることがわかります。また、グラフと y 軸との交点の座標から、 c も正であることがわかります。これで、2 や 5 は消去できます。
次に、頂点の座標から考えてみましょう。頂点の座標がわかるように、次のように平方完成をします。
\begin{eqnarray}
y
&=&
ax^2+bx+c \\[5pt]
&=&
a\left(x^2+\frac{b}{a}x\right)+c \\[5pt]
&=&
a\left(x+\frac{b}{2a}x\right)^2-\frac{b^2}{4a}+c \\[5pt]
&=&
a\left(x+\frac{b}{2a}x\right)^2+\frac{4ac-b^2}{4a} \\[5pt]
\end{eqnarray}このように計算できることから、頂点の座標は\[ \left(-\frac{b}{2a}, \frac{4ac-b^2}{4a}\right) \]となることがわかります。
頂点は第3象限にあることから、頂点の x 座標は負です。また、先ほど見たように a は正なので、 b は正であることがわかります。よって、選択肢の中で残るものは、 0 と 3 だけです。
a が正で、頂点の y 座標が負であることから、\[ 4ac-b^2 \lt 0 \]となることがわかります。これを満たすものは、選択肢3だとわかります。
よって、3が答えとなります。
解答
ア:3
参考
解答編 つづき
問題
(2) 次に、a, b の値を(1)の値のまま変えずに、c の値だけを変化させた。このときの頂点の移動について正しく述べたものを、次の 0~3 のうちから一つ選べ。 $\myBox{イ}$
0: 最初の位置から移動しない。
1: x 軸方向に移動する。
2: y 軸方向に移動する。
3: 原点を中心として回転移動する。
解説
先ほど見たように、頂点の座標は\[ \left(-\frac{b}{2a}, \frac{4ac-b^2}{4a}\right) \]です。
なので、 c を動かしたとき、頂点の x 座標は変わりません。 x 座標に c が含まれていないからです。
一方、頂点の y 座標は、\[ c-\frac{b^2}{4a} \]と同じなので、 c を動かせば、頂点の y 座標も同じように変化幅で動くことがわかります。
以上から、 c の値だけ動かした場合は、頂点は y 軸方向に移動する(上下に移動する)ことがわかります。
解答
イ:2
解答編 つづき
問題
(3) また、b, c の値を(1)の値のまま変えずに、a の値だけをグラフが下に凸の状態を維持するように変化させた。このとき、頂点は、 $a=\dfrac{b^2}{4c}$ のときは $\myBox{ウ}$ にあり、 それ以外のときは $\myBox{エ}$ を移動した。 $\myBox{ウ}$, $\myBox{エ}$ に当てはまるものを、次の 0~8 のうちから一つずつ選べ。ただし、同じものを選んでもよい。
0: 原点
1: x 軸上
2: y 軸上
3: 第3象限のみ
4: 第1象限と第3象限
5: 第2象限と第3象限
6: 第3象限と第4象限
7: 第2象限と第3象限と第4象限
8: すべての象限
解説
頂点の座標は\[ \left(-\frac{b}{2a}, \frac{4ac-b^2}{4a}\right) \]でした。そのため、\[ a=\frac{b^2}{4c} \]のときは、 $b^2=4ac$ なので、頂点の y 座標は $0$ となります。よって、頂点は x 軸上にあることがわかります。
選択肢の中には「原点」があるので、頂点が原点にくるかどうかを、確認しておきましょう。原点にくるには、頂点の x 座標も $0$ でないといけないので、 $b=0$ のときとなります。しかし、今、 b は (1) の値のまま動かさないので、原点を通ることはありません。よって、「原点」は答えではなく、「 x 軸上」が答えになります。
それ以外の場合に、どこを動きうるかを考えましょう。グラフが下に凸の状態のまま a の値を動かすということは、 a の値は正のままだ、ということです。 x 座標を見ると\[ -\frac{b}{2a} \]ですが、 a, b は正なので、今の条件で動かす限り、頂点の x 座標は負の値しかとらないことがわかります。よって、答えは「第3象限のみ」か「第2象限と第3象限」の2種類しかありえません。
頂点の y 座標が正になることがあるかどうか、を考えましょう。 y 座標は、(1)の値を具体的に代入すると
\begin{eqnarray}
\frac{4ac-b^2}{4a}
&=&
c-\frac{b^2}{4a} \\[5pt]
&=&
3-\frac{9}{4a} \\[5pt]
\end{eqnarray}となります。 a の値を大きくすれば、頂点の y 座標が正の値をとるようにでき、小さくすれば負の値をとるようにできるので、「第2象限と第3象限」が正しいとわかります。
解答
ウ:1
エ:5
解答編 つづき
問題
(4) 最初の a, b, c の値を変更して、下の図2のようなグラフを表示させた。このとき、a, c の値をこのまま変えずに、b の値だけを変化させても、頂点は第1象限および第2象限には移動しなかった。
その理由を、頂点の y 座標についての不等式を用いて説明せよ。解答は、解答欄 $\myBox{(あ)}$ に記述せよ。
解説
記述の問題です。
頂点の y 座標は、今まで求めてきた通り\[ \frac{4ac-b^2}{4a} \]です。 b を動かしたときに、式の値がどうなるかを考えてみましょう。
下に凸なので、 a は正です。また、 y 軸との交点を見ると、 c が負であることがわかります。なので、分子の $4ac$ は負です。また、分母は正です。そのため、 b をいくらにしても、 y 座標が正になることはないため、第1象限や第2象限に移動することはありません。
このことを、指定された条件を踏まえて書くようにしましょう。頂点の y 座標が負になることと、その根拠として「 $a\gt 0$ かつ $c\lt 0$ であること」を含めましょう。
解答
グラフが下に凸なので a は正で、グラフは y 軸と負の部分で交わっているから c は負である。
頂点の y 座標は、 $\dfrac{4ac-b^2}{4a}$ であり、\[ \dfrac{4ac-b^2}{4a} \leqq \dfrac{4ac}{4a} = c \lt 0\]が成り立つから、頂点の y 座標が正になることはないので、頂点は第1象限および第2象限には移動しない。
(解答終)