京都大学 理学部特色入試 2018年度 第4問 解説
(2017年11月に行われた特色入試の問題です。2018年に行われた特色入試の問題はこちら)
問題編
問題
自然数 k と n は互いに素で、 $k\lt n$ を満たすとする。 n 項からなる数列 $a_1,a_2,\cdots,a_n$ が次の3条件 (イ), (ロ), (ハ) を満たすとき、性質 $\mathrm{P}(k,n)$ を持つということにする。
(イ) $a_1,a_2,\cdots,a_n$ はすべて整数。
(ロ) $0\leqq a_1\lt a_2\lt \cdots \lt a_n \lt 2^n-1$
(ハ) $a_{n+1},\cdots a_{n+k}$ を $a_{n+j}=a_j$ $(1\leqq j \leqq k)$ で定めたとき、 n 以下のすべての自然数 m に対して $2a_m-a_{m+k}$ は $2^n-1$ で割り切れる。以下の設問に答えよ。
(1) $k=2$ かつ $n=5$ の場合を考える。性質 $\mathrm{P}(2,5)$ を持つ数列 $a_1,a_2,\cdots,a_5$ をすべて求めよ。
(2) 数列 $a_1,a_2,\cdots ,a_n$ が性質 $\mathrm{P}(k,n)$ を持つとする。 $a_{k+1}-a_k=1$ であることを示せ。
考え方
(1)は、ある程度、条件を絞って、必要条件から考えていくといいでしょう。(ハ)の条件をどう使うかがポイントです。 「 $2^n-1$ で割り切れる」と書かれていますが、 $2^n-1$ の何倍になるかを絞り込むことができます。
(2)は、数列を円形に並べてみると考えやすいかもしれません。 $a_k,a_{k+1}$ の差だけでなく、 $a_{2k},a_{2k+1}$ や $a_{3k},a_{3k+1}$ などがどうなるかを考えていきましょう。そうすると、「互いに素」の条件もどこで使うかが見えてきます。
解答編
問題
自然数 k と n は互いに素で、 $k\lt n$ を満たすとする。 n 項からなる数列 $a_1,a_2,\cdots,a_n$ が次の3条件 (イ), (ロ), (ハ) を満たすとき、性質 $\mathrm{P}(k,n)$ を持つということにする。
(イ) $a_1,a_2,\cdots,a_n$ はすべて整数。
(ロ) $0\leqq a_1\lt a_2\lt \cdots \lt a_n \lt 2^n-1$
(ハ) $a_{n+1},\cdots a_{n+k}$ を $a_{n+j}=a_j$ $(1\leqq j \leqq k)$ で定めたとき、 n 以下のすべての自然数 m に対して $2a_m-a_{m+k}$ は $2^n-1$ で割り切れる。以下の設問に答えよ。
(1) $k=2$ かつ $n=5$ の場合を考える。性質 $\mathrm{P}(2,5)$ を持つ数列 $a_1,a_2,\cdots,a_5$ をすべて求めよ。
解答
m を n 以下の自然数とする。
条件(イ)(ハ)より、 $2a_m -a_{m+k}$ は $2^n-1$ の整数倍である。また、条件(ロ)より、
\begin{eqnarray}
2a_m -a_{m+k} \leqq 2a_m \lt 2(2^n-1)
\end{eqnarray}であり、
\begin{eqnarray}
2a_m -a_{m+k} \geqq -a_{m+k} \gt -(2^n-1)
\end{eqnarray}である。これらから、「 $2a_m -a_{m+k}$ は、 $0$ または $2^n-1$ である」ことがわかる。
また、 $1\leqq m \leqq n-k$ のときは、条件(ロ)より、 $a_m \lt a_{m+k}$ なので、
\begin{eqnarray}
2a_m -a_{m+k}
&=&
a_m +(a_m-a_{m+k}) \\[5pt]
&\lt&
a_m \\[5pt]
&\lt&
2^n-1
\end{eqnarray}だから、 $2a_m -a_{m+k}=0$ である。
一方、 $n-k \lt m \leqq n$ のときは、条件(ハ)から、 $a_{m+k}=a_{m+k-n}$ であり、 $k\lt n$ より $m+k-n\lt m$ だから、条件(ロ)より、 $a_{m+k} \lt a_m$ が成り立つ。よって
\begin{eqnarray}
2a_m -a_{m+k}
&=&
a_m +(a_m-a_{m+k}) \\[5pt]
&\gt&
a_m \\[5pt]
&\geqq&
0
\end{eqnarray}なので、 $2a_m -a_{m+k}=2^n-1$ である。
以上のことから、 $a_1,a_2,\cdots,a_5$ が性質 $\mathrm{P}(2,5)$ を持つとすると、次が成り立つ。
\begin{eqnarray}
2a_1 -a_3 &=& 0 \\[5pt]
2a_2 -a_4 &=& 0 \\[5pt]
2a_3 -a_5 &=& 0 \\[5pt]
2a_4 -a_6 &=& 2^5-1 \\[5pt]
2a_5 -a_7 &=& 2^5-1 \\[5pt]
\end{eqnarray}これより、 $a_3=2a_1$, $a_4=2a_2$, $a_5=2a_3=4a_1$ が成り立つ。また、上の5つの式を辺々足すと、 $a_6=a_1$, $a_7=a_2$ となることも用いて、
\begin{eqnarray}
a_1+a_2+a_3+a_4+a_5 &=& 62 \\[5pt]
a_1+a_2+2a_1+2a_2+4a_1 &=& 62 \\[5pt]
7a_1+3a_2 &=& 62 \\[5pt]
\end{eqnarray}が成り立つことがわかる。 $0\lt a_2$ であることから、 $0\leqq a_1\leqq 8$ であることがわかる。さらに、 $a_2$ が整数であることより、 $a_1=2,5,8$ となり、 $a_1\lt a_2\lt a_3=2a_1$ を満たすものは、 $a_1=5$ のみであることがわかる。
こうして、性質 $\mathrm{P}(2,5)$ を満たすとすれば、 $a_1=5$, $a_2=9$, $a_3=10$, $a_4=18$, $a_5=20$ となることがわかる。逆に、この数列が条件(イ)(ロ)(ハ)を満たすことがわかるので、求める数列はこの数列のみ、となる。
(解答終)
問題
(2) 数列 $a_1,a_2,\cdots ,a_n$ が性質 $\mathrm{P}(k,n)$ を持つとする。 $a_{k+1}-a_k=1$ であることを示せ。
解答
$a_1,a_2,\cdots ,a_n$ を、時計回りの順番に、円形に並べる。このとき、 $a_1$ を $1$ 番目として、時計回りに数えて m 番目の数字を $a_m$ とする。このように、無限数列に拡張した数列を考えることにする。このとき、この数列は条件(イ)(ロ)(ハ)を満たす。また、すべての自然数 m について、 $a_{m+n}=a_m$ が成り立つ。
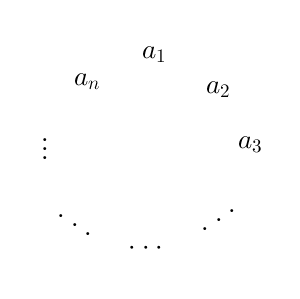
条件(ハ)より、すべての自然数 m に対して、「 $2a_m-a_{m+k}$ が $2^n-1$ で割り切れる」ことがわかる。また、(1)で示したように、 $2a_m-a_{m+k}$ は $0$ か $2^n-1$ であり、 $m+k-1$ を n で割った余りが $m-1$ を n で割った余りより大きい場合は $2a_m-a_{m+k}=0$, そうでない場合は $2a_m-a_{m+k}=2^n-1$ であることがわかる。
$k,n$ は互いに素なので、 $k,2k,\cdots,(n-1)k,nk$ を n で割った余りに同じものは含まれない。よって、 $a_k,a_{2k},\cdots,a_{(n-1)k},a_{nk}$ は、 $a_1,a_2,\cdots,a_n$ を並び替えたものとなる。また、番号を1つずらしても同じことが言えるため、 $a_{k+1},a_{2k+1},\cdots,a_{(n-1)k+1},a_{nk+1}$ も、 $a_1,a_2,\cdots,a_n$ を並び替えたものとなる。
$2\leqq m \leqq n$ のとき、 $(mk+1)-1$ を n で割った余りが $mk-1$ を n で割った余り以下となるのは、 $m=n$ のときだけである。このとき、
\begin{eqnarray}
a_{nk+1} &=& 2a_{(n-1)k+1} -(2^n-1) \\[5pt]
a_{nk} &=& 2a_{(n-1)k} \\[5pt]
\end{eqnarray}となる。これ以外の場合は、
\begin{eqnarray}
a_{mk+1}-a_{mk}=2a_{(m-1)k+1}-2a_{(m-1)k}
\end{eqnarray}となる。
このことから、
\begin{eqnarray}
a_{k+1}-a_k &=& a_{k+1}-a_k \\[5pt]
a_{2k+1}-a_{2k} &=& 2(a_{k+1}-a_k) \\[5pt]
a_{3k+1}-a_{3k} &=& 2^2(a_{k+1}-a_k) \\[5pt]
& \vdots & \\[5pt]
a_{(n-1)k+1}-a_{(n-1)k} &=& 2^{n-2}(a_{k+1}-a_k) \\[5pt]
a_{nk+1}-a_{nk} &=& 2^{n-1}(a_{k+1}-a_k) -(2^n-1) \\[5pt]
\end{eqnarray}が成り立つ。この n 個の式を辺々足すと、左辺は、「 $a_1,a_2,\cdots,a_n$ を並び替えたものの和」から「 $a_1,a_2,\cdots,a_n$ を並び替えたものの和」を引いたものになるため、 $0$ となる。一方、右辺は
\begin{eqnarray}
& &
(1+2+2^2+\cdots+2^{n-1})(a_{k+1}-a_k)-(2^n-1) \\[5pt]
&=&
(2^n-1)(a_{k+1}-a_k)-(2^n-1) \\[5pt]
&=&
(2^n-1)(a_{k+1}-a_k-1) \\[5pt]
\end{eqnarray}となる。これが $0$ となることと、 $2^n-1\ne 0$ より、 $a_{k+1}-a_k-1=0$ となる。よって、\[ a_{k+1}-a_k=1 \]となる。
(解答終)
解説
(2)の内容を、(1)を使って具体的に考えてみましょう。円形に並べてみると、次のようになります。
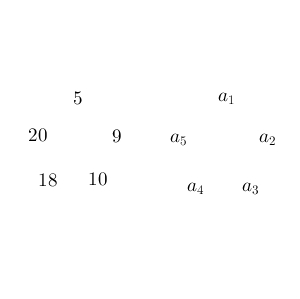
ここで、 $m=1,2,\cdots,n$ として、 $a_{mk},a_{mk+1}$ を順に考えてみると、次のようになります。
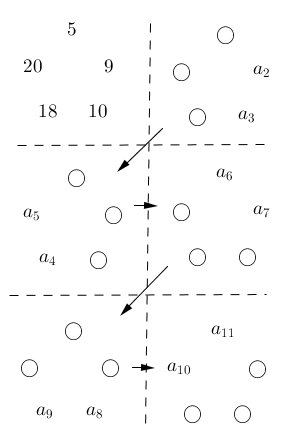
この差は、 m が進むごとに2倍されていき、最後の $a_{nk+1}-a_{nk}$ のときだけ、「2倍したものから $2^n-1$ を引いたもの」になります。また、この差を m について足すと $0$ になります。このことを一般的な状況で書いたものが(2)の解答となります。





