京都大学 理系 2016年度 第5問 解説
問題編
【問題】
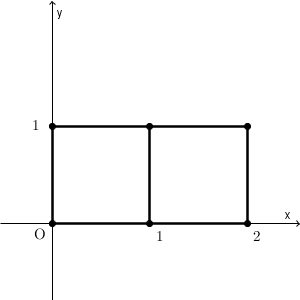
xy平面上の6個の点$(0,0)$、$(0,1)$、$(1,0)$、$(1,1)$、$(2,0)$、$(2,1)$が図のように長さ1の線分で結ばれている。動点Xは、これらの点の上を次の規則に従って1秒ごとに移動する。規則:動点Xは、そのときに位置する点から出る長さ1の線分によって結ばれる図の点のいずれかに、等しい確率で移動する。
例えば、Xが$(2,0)$にいるときは、$(1,0)$、$(2,1)$のいずれかに$\displaystyle \frac{1}{2}$の確率で移動する。またXが$(1,1)$にいるときは、$(0,1)$、$(1,0)$、$(2,1)$のいずれかに$\displaystyle \frac{1}{3}$の確率で移動する。
時刻0で動点Xが$\mathrm{ O }=(0,0)$から出発するとき、n秒後にXのx座標が0である確率を求めよ。ただしnは0以上の整数とする。
【考え方】
(0,0)にいるとき、次の移動でx座標が0,1になる確率がそれぞれ$\frac{1}{2}$で、(0,1)にいるときも次の移動でx座標が0,1になる確率はそれぞれ$\frac{1}{2}$になります。つまり、x座標だけに着目すれば、2つの点をまとめて考えることができます。求める確率も、(0,0)にいる確率ではなく、x座標が0である確率なので、まとめたまま考えることができます。
つまり、x座標が0,1,2である確率をそれぞれ求めればOKです。3つの確率を足すと1になるので、x座標が0,2である確率を考えるだけでよく、うまく2つの漸化式を作れば、答えにたどり着けます。
解答編
【問題】
xy平面上の6個の点$(0,0)$、$(0,1)$、$(1,0)$、$(1,1)$、$(2,0)$、$(2,1)$が図のように長さ1の線分で結ばれている。動点Xは、これらの点の上を次の規則に従って1秒ごとに移動する。規則:動点Xは、そのときに位置する点から出る長さ1の線分によって結ばれる図の点のいずれかに、等しい確率で移動する。
例えば、Xが$(2,0)$にいるときは、$(1,0)$、$(2,1)$のいずれかに$\displaystyle \frac{1}{2}$の確率で移動する。またXが$(1,1)$にいるときは、$(0,1)$、$(1,0)$、$(2,1)$のいずれかに$\displaystyle \frac{1}{3}$の確率で移動する。
時刻0で動点Xが$\mathrm{ O }=(0,0)$から出発するとき、n秒後にXのx座標が0である確率を求めよ。ただしnは0以上の整数とする。
【解答】
n秒後にXのx座標が0,1,2である確率を、それぞれ$p_n,q_n,r_n$とおく。このとき、次の式が成り立つ。
ここで、(1)-(3)より
\begin{eqnarray}
p_{n+1} -r_{n+1} &=& \frac{1}{2}\left( p_n -r_n \right) \\[5pt]
p_n -r_n &=& \frac{1}{2^n}( p_0 -r_0 ) = \frac{1}{2^n} \quad \cdots (4)
\end{eqnarray}が得られる。
また、(1)+(3)より\[ p_{n+1} +r_{n+1} = \frac{1}{2}\left( p_n +r_n \right) +\frac{2}{3}q_n \]となるが、$q_n=1-p_n-r_n$なので、
\begin{eqnarray}
p_{n+1} +r_{n+1} &=& -\frac{1}{6}\left( p_n +r_n \right) +\frac{2}{3} \\[5pt]
p_{n+1} +r_{n+1} -\frac{4}{7} &=& -\frac{1}{6}\left( p_n +r_n -\frac{4}{7} \right) \\[5pt]
p_n +r_n -\frac{4}{7} &=& \left(-\frac{1}{6} \right)^n \left( p_0 +r_0 -\frac{4}{7} \right) \\[5pt]
p_n +r_n &=& \left(-\frac{1}{6} \right)^n \frac{3}{7} +\frac{4}{7} \quad \cdots (5)
\end{eqnarray}が得られる。
(4)+(5)より、
\begin{eqnarray}
2p_n &=& \frac{1}{2^n} +\left(-\frac{1}{6} \right)^n \frac{3}{7} +\frac{4}{7} \\[5pt]
p_n &=& \frac{1}{2^{n+1} } +\left(-\frac{1}{6} \right)^n \frac{3}{14} +\frac{2}{7}
\end{eqnarray}となる。
よって、求める確率は、$\displaystyle \frac{1}{2^{n+1} } +\left(-\frac{1}{6} \right)^n \frac{3}{14} +\frac{2}{7}$となる。
【解答終】
【解説】
6つの点について確率を求めようとすると、さすがに計算が大変すぎます。
6つ点がありますが、実はy座標が0の点と1の点を区別することに、あまり意味はありません。「その点にいるか、左右に1動くか」を考えるのと同じ、x座標だけに注目して考えればよい、ということに気づけないと漸化式を作ることができません。漸化式を作るまでが少し難しいですね。