センター試験数学II・数学B 2014年度追試第4問解説

🕒 2017/02/06 🔄 2023/05/01

【選択問題】(第3問～第6問から2問選択)

問題編

問題

　$\def\myBox#1{\bbox[3px, border:2px solid]{\ \bf{ #1 }\ } }\def\mybox#1{\bbox[4px, border:1px solid gray]{\ #1\ } }$平面上に、1辺の長さが $1$ の正方形 ABCD と、その外側に三角形 OAB があり、 $\displaystyle \mathrm{ OA }=\mathrm{ OB }=\frac{\sqrt{5} }{2}$ とする。 $0\lt t \lt 1$ とし、線分 OA, AD, CB を $t:(1-t)$ に内分する点をそれぞれ P, Q, R とする。以下では、 $\overrightarrow{ \mathrm{ OA } }=\vec{a}$, $\overrightarrow{ \mathrm{ OB } } = \vec{b}$ とおく。

(1) $|\vec{a}-\vec{b}|^2 = \myBox{ア}$ により、 $\displaystyle \vec{a}\cdot\vec{b}=\frac{\myBox{イ} }{\myBox{ウ} }$ である。また、 $\vec{a}+\vec{b}$ と $\overrightarrow{ \mathrm{ AD } }$ は平行であり、 $|\vec{a}+\vec{b}| = \myBox{エ}$ により、 $\displaystyle \overrightarrow{ \mathrm{ AD } }=\frac{\myBox{オ} }{\myBox{カ} } (\vec{a}+\vec{b})$ である。

　次に、 $\overrightarrow{ \mathrm{ PQ } }$, $\overrightarrow{ \mathrm{ PR } }$ を t と $\vec{a}$, $\vec{b}$ を用いて表すと
\begin{eqnarray} & & \overrightarrow{ \mathrm{ PQ } } = \frac{\myBox{キ}-t}{\myBox{ク} } \vec{a} +\frac{t}{\mybox{ク} }\vec{b} \quad & \cdots ① \\[5pt] & & \overrightarrow{ \mathrm{ PR } } = \frac{1-\myBox{ケ}t}{\mybox{ク} } \vec{a} +\frac{\myBox{コ}-t}{\mybox{ク} }\vec{b} \quad & \cdots ② \\[5pt] \end{eqnarray}である。
(2) $0\lt t \lt 1$ の範囲において、三角形 PQR の面積 S の最小値を求めよう。点 P から線分 CD に引いた垂線と線分 QR の交点を T とする。三角形 PTQ と三角形 PTR の面積の和は S に等しいから、 $\displaystyle S=\frac{\myBox{サ} }{\myBox{シ} }\mathrm{ PT }$ である。これにより、 PT が最小になるときを考えればよいことがわかる。

　まず、 $\mathrm{ QT }:\mathrm{ TR } = (1-t):\myBox{ス}$ であるから\[ \overrightarrow{ \mathrm{ PT } } = \myBox{セ}\overrightarrow{ \mathrm{ PQ } } +\myBox{ソ}\overrightarrow{ \mathrm{ PR } } \quad \cdots ③ \]である。 $\myBox{ス}$, $\myBox{セ}$, $\myBox{ソ}$ に当てはまるものを、次の 0 ～ 7 のうちから一つずつ選べ。ただし、同じものを繰り返し選んでもよい。

　0: $t$
　1: $(1-t)$
　2: $(1+t)$
　3: $(1+2t)$
　4: $\frac{t}{2}$
　5: $\frac{1-t}{2}$
　6: $\frac{1+t}{2}$
　7: $\frac{1+2t}{2}$

したがって、①, ②, ③により\[ \overrightarrow{ \mathrm{ PT } } = \left(\frac{\myBox{タ} }{\myBox{チ} } t^2 -\frac{\myBox{ツ} }{\myBox{テ} } t +\frac{3}{4}\right) (\vec{a}+\vec{b}) \]となる。よって、 $\displaystyle t=\frac{\myBox{ト} }{\myBox{ナ} }$ のとき、 PT は最小となり、三角形 PQR の面積 S の最小値は $\displaystyle \frac{\myBox{ニヌ} }{\myBox{ネノ} }$ である。

考え方

図を正しく描いて考えれば難しくはないでしょう。

(1)の前半は、線分の長さや内積をからめた問題です。エは内積を使っても出せますし、長さを直接求めて出すこともできます。後半は、それぞれのベクトルを分解して考えていきましょう。

(2)の前半は、図をかいて考えましょう。後半は計算がメインですが、計算量はそれほど多くありません。最小値は平方完成をするか、微分をして求めましょう。

【選択問題】(第3問～第6問から2問選択)

解答編

問題

　$\def\myBox#1{\bbox[3px, border:2px solid]{\ \bf{ #1 }\ } }\def\mybox#1{\bbox[4px, border:1px solid gray]{\ #1\ } }$平面上に、1辺の長さが $1$ の正方形 ABCD と、その外側に三角形 OAB があり、 $\displaystyle \mathrm{ OA }=\mathrm{ OB }=\frac{\sqrt{5} }{2}$ とする。 $0\lt t \lt 1$ とし、線分 OA, AD, CB を $t:(1-t)$ に内分する点をそれぞれ P, Q, R とする。以下では、 $\overrightarrow{ \mathrm{ OA } }=\vec{a}$, $\overrightarrow{ \mathrm{ OB } } = \vec{b}$ とおく。

解説

図は次のようになっています。

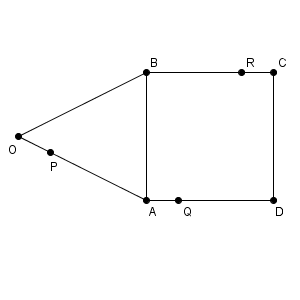
解答編つづき

問題

(1) $|\vec{a}-\vec{b}|^2 = \myBox{ア}$ により、 $\displaystyle \vec{a}\cdot\vec{b}=\frac{\myBox{イ} }{\myBox{ウ} }$ である。また、 $\vec{a}+\vec{b}$ と $\overrightarrow{ \mathrm{ AD } }$ は平行であり、 $|\vec{a}+\vec{b}| = \myBox{エ}$ により、 $\displaystyle \overrightarrow{ \mathrm{ AD } }=\frac{\myBox{オ} }{\myBox{カ} } (\vec{a}+\vec{b})$ である。

解説

\begin{eqnarray} \vec{a}-\vec{b} &=& \overrightarrow{ \mathrm{ OA } }-\overrightarrow{ \mathrm{ OB } } \\ &=& \overrightarrow{ \mathrm{ BA } } \\ \end{eqnarray}なので、 $|\vec{a}-\vec{b}|^2=\mathrm{ AB }^2=1$ となります。

これより
\begin{eqnarray} |\vec{a}-\vec{b}|^2 &=& 1 \\[5pt] |\vec{a}|^2 -2\vec{a}\cdot \vec{b} +|\vec{b}|^2 &=& 1 \\[5pt] \frac{5}{4} -2\vec{a}\cdot \vec{b} +\frac{5}{4} &=& 1 \\[5pt] -2\vec{a}\cdot \vec{b} &=& -\frac{3}{2} \\[5pt] \vec{a}\cdot \vec{b} &=& \frac{3}{4} \\[5pt] \end{eqnarray}が得られます。

また
\begin{eqnarray} |\vec{a}+\vec{b}|^2 &=& |\vec{a}|^2 +2\vec{a}\cdot \vec{b} +|\vec{b}|^2 \\[5pt] &=& \frac{5}{4} +2\times \frac{3}{4} +\frac{5}{4} \\[5pt] &=& 4 \\[5pt] \end{eqnarray}なので、 $|\vec{a}+\vec{b}|=2$ となります。

$\mathrm{ OA }=\mathrm{ OB }$ なので、 $\vec{a}+\vec{b}$ と $\overrightarrow{ \mathrm{ AD } }$ は平行であり、ベクトルの大きさが $2:1$ なので\[ \overrightarrow{ \mathrm{ AD } } = \frac{1}{2}(\vec{a}+\vec{b}) \]となります。

解答

アイウ：134
エオカ：212

解答編つづき

問題

　次に、 $\overrightarrow{ \mathrm{ PQ } }$, $\overrightarrow{ \mathrm{ PR } }$ を t と $\vec{a}$, $\vec{b}$ を用いて表すと
\begin{eqnarray} & & \overrightarrow{ \mathrm{ PQ } } = \frac{\myBox{キ}-t}{\myBox{ク} } \vec{a} +\frac{t}{\mybox{ク} }\vec{b} \quad & \cdots ① \\[5pt] & & \overrightarrow{ \mathrm{ PR } } = \frac{1-\myBox{ケ}t}{\mybox{ク} } \vec{a} +\frac{\myBox{コ}-t}{\mybox{ク} }\vec{b} \quad & \cdots ② \\[5pt] \end{eqnarray}である。

解説

\begin{eqnarray} \overrightarrow{ \mathrm{ PQ } } &=& -\overrightarrow{ \mathrm{ OP } } +\overrightarrow{ \mathrm{ OQ } } \\[5pt] &=& -t\vec{a} +\overrightarrow{ \mathrm{ OA } }+\overrightarrow{ \mathrm{ AQ } } \\[5pt] &=& -t\vec{a} +\vec{a}+t\overrightarrow{ \mathrm{ AD } } \\[5pt] &=& -t\vec{a} +\vec{a}+t \times \frac{1}{2}(\vec{a}+\vec{b}) \\[5pt] &=& \frac{-2t+2+t}{2}\vec{a} +\frac{t}{2}\vec{b} \\[5pt] &=& \frac{2-t}{2}\vec{a} +\frac{t}{2}\vec{b} \\[5pt] \end{eqnarray}となります。

また、
\begin{eqnarray} \overrightarrow{ \mathrm{ PR } } &=& -\overrightarrow{ \mathrm{ OP } } +\overrightarrow{ \mathrm{ OR } } \\[5pt] &=& -t\vec{a} +\overrightarrow{ \mathrm{ OB } }+\overrightarrow{ \mathrm{ BR } } \\[5pt] &=& -t\vec{a} +\vec{b}+(1-t) \overrightarrow{ \mathrm{ BC } } \\[5pt] &=& -t\vec{a} +\vec{b}+(1-t) \times \frac{1}{2}(\vec{a}+\vec{b}) \\[5pt] &=& \frac{-2t+(1-t)}{2}\vec{a} +\frac{2+(1-t)}{2}\vec{b} \\[5pt] &=& \frac{1-3t}{2}\vec{a} +\frac{3-t}{2}\vec{b} \\[5pt] \end{eqnarray}となります。

解答

キク：22
ケコ：33

解答編つづき

問題

(2) $0\lt t \lt 1$ の範囲において、三角形 PQR の面積 S の最小値を求めよう。点 P から線分 CD に引いた垂線と線分 QR の交点を T とする。三角形 PTQ と三角形 PTR の面積の和は S に等しいから、 $\displaystyle S=\frac{\myBox{サ} }{\myBox{シ} }\mathrm{ PT }$ である。これにより、 PT が最小になるときを考えればよいことがわかる。

解説

図は次のようになっています。P から CD に引いた垂線の足を E としています。

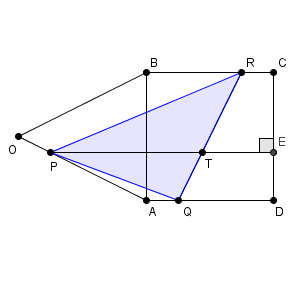
三角形PQR を、三角形PTQ と三角形PTR に分割し、 PT を底辺と考えると、高さはそれぞれ DE, CE となります。よって、高さの和は t の値に関係なく $1$ となるので、
\begin{eqnarray} S &=& \frac{1}{2} \mathrm{ PT }(\mathrm{ CE }+\mathrm{ DE }) \\[5pt] &=& \frac{1}{2} \mathrm{ PT } \\[5pt] \end{eqnarray}となります。

解答

サシ：12

解答編つづき

問題

　まず、 $\mathrm{ QT }:\mathrm{ TR } = (1-t):\myBox{ス}$ であるから\[ \overrightarrow{ \mathrm{ PT } } = \myBox{セ}\overrightarrow{ \mathrm{ PQ } } +\myBox{ソ}\overrightarrow{ \mathrm{ PR } } \quad \cdots ③ \]である。 $\myBox{ス}$, $\myBox{セ}$, $\myBox{ソ}$ に当てはまるものを、次の 0 ～ 7 のうちから一つずつ選べ。ただし、同じものを繰り返し選んでもよい。

　0: $t$
　1: $(1-t)$
　2: $(1+t)$
　3: $(1+2t)$
　4: $\frac{t}{2}$
　5: $\frac{1-t}{2}$
　6: $\frac{1+t}{2}$
　7: $\frac{1+2t}{2}$

解説

\begin{eqnarray} \mathrm{ QT } : \mathrm{ RT } &=& \mathrm{ AP } : (\mathrm{ PO }+\mathrm{ OB }) \\ &=& (1-t) : (t+1) \\ \end{eqnarray}となるので、 $\mathrm{ QT }:\mathrm{ TR } = (1-t):(1+t)$ となります。

これより
\begin{eqnarray} \overrightarrow{ \mathrm{ PT } } &=& \frac{1+t}{(1-t)+(1+t)} \overrightarrow{ \mathrm{ PQ } } +\frac{1-t}{(1-t)+(1+t)} \overrightarrow{ \mathrm{ PR } } \\[5pt] &=& \frac{1+t}{2} \overrightarrow{ \mathrm{ PQ } } +\frac{1-t}{2} \overrightarrow{ \mathrm{ PR } } \\[5pt] \end{eqnarray}となります。

解答

スセソ：265

解答編つづき

問題

したがって、①, ②, ③により\[ \overrightarrow{ \mathrm{ PT } } = \left(\frac{\myBox{タ} }{\myBox{チ} } t^2 -\frac{\myBox{ツ} }{\myBox{テ} } t +\frac{3}{4}\right) (\vec{a}+\vec{b}) \]となる。よって、 $\displaystyle t=\frac{\myBox{ト} }{\myBox{ナ} }$ のとき、 PT は最小となり、三角形 PQR の面積 S の最小値は $\displaystyle \frac{\myBox{ニヌ} }{\myBox{ネノ} }$ である。

解説

①と②を③に代入すると
\begin{eqnarray} \overrightarrow{ \mathrm{ PT } } &=& \frac{1+t}{2} \left(\frac{2-t}{2}\vec{a} +\frac{t}{2}\vec{b}\right) \\[5pt] & & +\frac{1-t}{2} \left(\frac{1-3t}{2}\vec{a} +\frac{3-t}{2}\vec{b}\right) \\[5pt] &=& \left(\frac{1+t}{2}\times \frac{2-t}{2} +\frac{1-t}{2} \times \frac{1-3t}{2}\right) \vec{a} \\[5pt] & & +\left(\frac{1+t}{2}\times \frac{t}{2} +\frac{1-t}{2} \times \frac{3-t}{2}\right) \vec{b} \\[5pt] &=& \frac{(-t^2+t+2)+(3t^2-4t+1)}{4} \vec{a} \\[5pt] & & +\frac{(t^2+t)+(t^2-4t+3)}{4} \vec{b} \\[5pt] &=& \frac{2t^2-3t+3}{4} \vec{a}+\frac{2t^2-3t+3}{4} \vec{b} \\[5pt] &=& \left(\frac{1}{2}t^2-\frac{3}{4}t+\frac{3}{4}\right) (\vec{a}+\vec{b}) \\[5pt] \end{eqnarray}となります。

1つ目のカッコの中を平方完成すると
\begin{eqnarray} & & \frac{1}{2}t^2-\frac{3}{4}t+\frac{3}{4} \\[5pt] &=& \frac{1}{2} \left(t^2-\frac{3}{2}t+\frac{3}{2}\right) \\[5pt] &=& \frac{1}{2} \left\{\left(t-\frac{3}{4}\right)^2 -\frac{9}{16}+\frac{3}{2}\right\} \\[5pt] &=& \frac{1}{2} \left(t-\frac{3}{4}\right)^2 +\frac{1}{2}\times\frac{-9+24}{16} \\[5pt] &=& \frac{1}{2} \left(t-\frac{3}{4}\right)^2 +\frac{15}{32} \\[5pt] \end{eqnarray}となるので、PT が最小となるのは $\displaystyle t=\frac{3}{4}$ のときであることがわかります。

このとき、\[ \overrightarrow{ \mathrm{ PT } }=\frac{15}{32}(\vec{a}+\vec{b}) \]であり、エより $|\vec{a}+\vec{b}|=2$ なので、 $\displaystyle \mathrm{ PT }=\frac{15}{16}$ となります。サシより $\displaystyle S=\frac{1}{2}\mathrm{ PT }$ なので、このときの S は $\displaystyle \frac{15}{32}$ となります。