センター試験 数学II・数学B 2014年度追試 第1問 [1] 解説
【必答問題】
問題編
問題
$\def\myBox#1{\bbox[3px, border:2px solid]{\ \bf{ #1 }\ } }\def\mybox#1{\bbox[4px, border:1px solid gray]{\ #1\ } }$不等式\[ 4\left\{ \log_2(3-\sqrt{x}) \right\}^2 +3\log_{\frac{1}{8} }(3-\sqrt{x})^2 -2 \gt 0 \quad \cdots ① \]を満たす x のとり得る値の範囲を求めよう。
まず、真数は正であるから\[ 0\leqq x \lt \myBox{ア} \quad \cdots ② \]である。ただし、対数 $\log_a b$ に対し、 a を底といい、 b を真数という。
$y=\log_{\frac{1}{8} } (3-\sqrt{x})^2$ とおくと、 $\displaystyle \left(\frac{1}{8}\right)^y = (3-\sqrt{x})^2$ である。 $2$ を底とする両辺の対数をとれば\[ y=-\frac{\myBox{イ} }{\myBox{ウ} } \log_2(3-\sqrt{x}) \]であることがわかる。
よって、 $X=\log_2(3-\sqrt{x})$ とおくと、①は\[ \myBox{エ}X^2 -X-1 \gt 0 \quad \cdots ③ \]と表すことができる。
不等式③を解くと\[ X\lt -\frac{1}{\myBox{オ} }, \quad X \gt \myBox{カ} \]となり、 $X=\log_2(3-\sqrt{x})$ により\[ 3-\sqrt{x} \lt \frac{\sqrt{\myBox{キ} }}{\myBox{ク} }, \quad 3-\sqrt{x}\gt \myBox{ケ} \quad \cdots ④ \]であることがわかる。②と④から、不等式①を満たす x のとり得る値の範囲は\[ 0\leqq x \lt \myBox{コ}, \ \frac{\myBox{サシ} }{\myBox{ス} }-\myBox{セ}\sqrt{\mybox{キ} } \lt x \lt \mybox{ア} \]である。
考え方
いきなりよくわからない不等式から始まりますが、その後の誘導は丁寧です。言われた通りに変形したり文字で置き換えたりすることで、与えられた不等式が解けるようになります。対数の計算がきちんとできるようになっていないと解けませんが、計算の量自体は少ないです。最後は数直線を使って考えたほうが分かりやすいでしょう。
【必答問題】
解答編
問題
$\def\myBox#1{\bbox[3px, border:2px solid]{\ \bf{ #1 }\ } }\def\mybox#1{\bbox[4px, border:1px solid gray]{\ #1\ } }$不等式\[ 4\left\{ \log_2(3-\sqrt{x}) \right\}^2 +3\log_{\frac{1}{8} }(3-\sqrt{x})^2 -2 \gt 0 \quad \cdots ① \]を満たす x のとり得る値の範囲を求めよう。
まず、真数は正であるから\[ 0\leqq x \lt \myBox{ア} \quad \cdots ② \]である。ただし、対数 $\log_a b$ に対し、 a を底といい、 b を真数という。
解説
真数は正なので、 $\log_2(3-\sqrt{x})$ のカッコの部分は正でないといけません。よって
\begin{eqnarray}
3-\sqrt{x} & \gt & 0 \\
\sqrt{x} & \lt & 3 \\
\end{eqnarray}となり、両辺を2乗して\[ x \lt 9 \]が得られます。ルートの中は0以上でないといけないので、 x の範囲は\[ 0 \leqq x \lt 9 \]となります。
真数の説明が書いてありますが、この説明がなくても真数が何かはわかるようになっておきましょう。また、二次試験では、「真数が正」という条件を考慮するように明記されていることはほとんどありませんが、自分で真数条件を考えないといけません。
解答
ア:9
解答編 つづき
問題
$y=\log_{\frac{1}{8} } (3-\sqrt{x})^2$ とおくと、 $\displaystyle \left(\frac{1}{8}\right)^y = (3-\sqrt{x})^2$ である。 $2$ を底とする両辺の対数をとれば\[ y=-\frac{\myBox{イ} }{\myBox{ウ} } \log_2(3-\sqrt{x}) \]であることがわかる。
解説
$\displaystyle \left(\frac{1}{8}\right)^y = (3-\sqrt{x})^2$ の左辺は
\begin{eqnarray}
\left(\frac{1}{8}\right)^y
&=&
\left( 2^{-3} \right)^y \\[5pt]
&=&
2^{-3y} \\[5pt]
\end{eqnarray}なので、 $2$ を底とする両辺の対数をとると
\begin{eqnarray}
-3y &=& \log_2 (3-\sqrt{x})^2 \\
&=& 2\log_2 (3-\sqrt{x}) \\[5pt]
y &=& -\frac{2}{3}\log_2 (3-\sqrt{x}) \\
\end{eqnarray}となります。
解答
イウ:23
解答編 つづき
問題
よって、 $X=\log_2(3-\sqrt{x})$ とおくと、①は\[ \myBox{エ}X^2 -X-1 \gt 0 \quad \cdots ③ \]と表すことができる。
解説
先ほどの結果を①に代入すると
\begin{eqnarray}
4\left\{ \log_2(3-\sqrt{x}) \right\}^2 +3\log_{\frac{1}{8} }(3-\sqrt{x})^2 -2 & \gt & 0 \\
4\left\{ \log_2(3-\sqrt{x}) \right\}^2 +3 \times \left(-\frac{2}{3}\right)\log_2 (3-\sqrt{x}) -2 & \gt & 0 \\
4\left\{ \log_2(3-\sqrt{x}) \right\}^2 -2\log_2 (3-\sqrt{x}) -2 & \gt & 0 \\
\end{eqnarray}となるので、 $X=\log_2(3-\sqrt{x})$ とおくと
\begin{eqnarray}
4X^2 -2X -2 & \gt & 0 \\
2X^2 -X -1 & \gt & 0 \\
\end{eqnarray}となります。
解答
エ:2
解答編 つづき
問題
不等式③を解くと\[ X\lt -\frac{1}{\myBox{オ} }, \quad X \gt \myBox{カ} \]となり、 $X=\log_2(3-\sqrt{x})$ により\[ 3-\sqrt{x} \lt \frac{\sqrt{\myBox{キ} }}{\myBox{ク} }, \quad 3-\sqrt{x}\gt \myBox{ケ} \quad \cdots ④ \]であることがわかる。
解説
不等式③は
\begin{eqnarray}
2X^2 -X -1 & \gt & 0 \\
(2X+1)(X-1) & \gt & 0 \\
\end{eqnarray}と変形できます。 $y=2X^2 -X -1$ のグラフは、次のようになります。
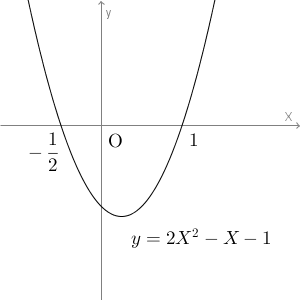
よって、この不等式の解は\[ X\lt-\frac{1}{2}, \ X\gt 1 \]となります。
$X=\log_2(3-\sqrt{x})$ だったので、これを1つ目の式に代入すると
\begin{eqnarray}
\log_2(3-\sqrt{x}) & \lt & -\frac{1}{2} \\[5pt]
& = & \log_2 2^{-\frac{1}{2} } \\[5pt]
& = & \log_2 \frac{\sqrt{2} }{2} \\[5pt]
\end{eqnarray}となります。底が1より大きいので、これから\[ 3-\sqrt{x} \lt \frac{\sqrt{2} }{2} \]が得られます。
また、不等式の解の2つ目の式に代入すると
\begin{eqnarray}
\log_2(3-\sqrt{x}) & \gt & 1 \\[5pt]
& = & \log_2 2^1 \\[5pt]
& = & \log_2 2 \\[5pt]
\end{eqnarray}となります。底が1より大きいので、これから\[ 3-\sqrt{x} \gt 2 \]が得られます。
解答
オカ:21
キクケ:222
解答編 つづき
問題
②と④から、不等式①を満たす x のとり得る値の範囲は\[ 0\leqq x \lt \myBox{コ}, \ \frac{\myBox{サシ} }{\myBox{ス} }-\myBox{セ}\sqrt{\mybox{キ} } \lt x \lt \mybox{ア} \]である。
解説
真数条件から\[ 0 \leqq x \lt 9 \]であり、与えられた不等式から\[ 3-\sqrt{x} \lt \frac{\sqrt{2} }{2}, \ 3-\sqrt{x} \gt 2 \]が得られました。
まず、 $3-\sqrt{x}$ で書かれた条件を変形しましょう。1つ目の条件式は
\begin{eqnarray}
3-\sqrt{x} & \lt & \frac{\sqrt{2} }{2} \\[5pt]
3-\frac{\sqrt{2} }{2} & \lt & \sqrt{x} \\[5pt]
\end{eqnarray}と変形でき、両辺正なので2乗して
\begin{eqnarray}
\left(3-\frac{\sqrt{2} }{2}\right)^2 & \lt & x \\[5pt]
9-3\sqrt{2}+\frac{1}{2} & \lt & x \\[5pt]
\frac{19}{2}-3\sqrt{2} & \lt & x \\[5pt]
\end{eqnarray}と変形できます。
また、2つ目の条件式は
\begin{eqnarray}
3-\sqrt{x} & \gt & 2 \\
3-2 & \gt & \sqrt{x} \\
1 & \gt & \sqrt{x} \\
\end{eqnarray}から $x\lt 1$ が得られます。
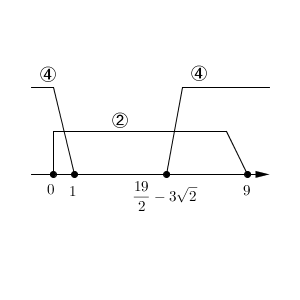
これらの条件をまとめると、 x のとり得る範囲は\[ 0\leqq x \lt 1, \ \frac{19}{2}-3\sqrt{2} \lt x \lt 9 \]となることがわかります。
解答
コ:1
サシスセ:1923





