センター試験 数学I・数学A 2006年度 第3問 解説
問題編
【問題】
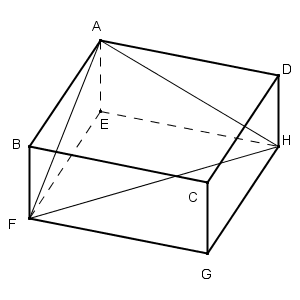
下の図のような直方体ABCD-EFGHにおいて、\[ \mathrm{ AE }=\sqrt{10}, \mathrm{ AF }=8, \mathrm{ AH }=10 \]とする。このとき、$\mathrm{ FH }=[アイ]$であり、$\displaystyle \cos\angle \mathrm{ FAH }=\frac{[ウ]}{[エ]}$である。また、三角形AFHの面積は$[オカ]\sqrt{[キ]}$である。
次に、$\angle\mathrm{ AFH }$の二等分線と辺AHの交点をP、$\angle\mathrm{ FAH }$に二等分線と辺FHの交点をQ、線分FPと線分AQの交点をRとする。このとき、Rは三角形AFHの[ク]である。次の0~2のうちから[ク]に当てはまるものを一つ選べ。
0: 重心、 1: 外心、 2: 内心
(補足説明:三角形において、その外接円の中心を外心、その内接円の中心を内心という。)また、$\mathrm{ AP }=[ケ]$であり、したがって、\[ \mathrm{ PF }:\mathrm{ PR } = [コ]:1 \]となる。さらに、四面体EAPRの体積は$[サ]\sqrt{[シ]}$である。
【考え方】
見た感じ「うっ」となってしまいそうな直方体の図ですが、ほとんどは三角形の問題です。落ち着いて解いていきましょう。
前半は、三平方の定理、余弦定理、$\sin$と$\cos$の関係を使って解いていきます。
後半は図が見にくいですが、三角形AFHを抜き出してくれば、考えやすくなるかもしれません。最後の四面体の体積は、直接求めるのは大変です。体積を求めやすい四面体があるので、それを使って比で求めていくと解きやすいです。
解答編
【問題】
下の図のような直方体ABCD-EFGHにおいて、\[ \mathrm{ AE }=\sqrt{10}, \mathrm{ AF }=8, \mathrm{ AH }=10 \]とする。このとき、$\mathrm{ FH }=[アイ]$であり、$\displaystyle \cos\angle \mathrm{ FAH }=\frac{[ウ]}{[エ]}$である。また、三角形AFHの面積は$[オカ]\sqrt{[キ]}$である。
【解説】
FHの長さを求めるには、三角形EFHで三平方の定理を使えば求められます。EFの長さは、三角形AEFで三平方の定理を使うと、\[ \mathrm{ EF } = \sqrt{8^2-(\sqrt{10})^2}=\sqrt{54} \]となります。また、EHの長さは、三角形AEHで三平方の定理を使うと、\[ \mathrm{ EH } = \sqrt{10^2-(\sqrt{10})^2}=\sqrt{90} \]となります。
これらのことから、三角形EFHで三平方の定理を使えば\[ \mathrm{ FH } = \sqrt{(\sqrt{54})^2+(\sqrt{90})^2}=\sqrt{144}=12 \]となります。
三角形AFHについて余弦定理を適用すると
\begin{eqnarray}
\cos\angle \mathrm{ FAH }
&=&
\frac{ 8^2 +10^2 -12^2 }{2 \cdot 8 \cdot 10} \\[5pt]
&=&
\frac{ 20 }{2 \cdot 8 \cdot 10} \\[5pt]
&=&
\frac{ 1 }{8}
\end{eqnarray}となります。
三角形AFHの面積は、$\displaystyle \frac{1}{2}\mathrm{ AF }\cdot \mathrm{ AH }\sin\angle \mathrm{ FAH }$で求めることができます。$\cos$の値は先ほど求めたので、
\begin{eqnarray}
\sin\angle \mathrm{ FAH }
&=&
\sqrt{1-\left(\frac{1}{8}\right)^2} \\[5pt]
&=&
\frac{3\sqrt{7} }{8}
\end{eqnarray}となります。よって、三角形AFHの面積は、
\begin{eqnarray}
\frac{1}{2}\mathrm{ AF }\cdot \mathrm{ AH }\sin\angle \mathrm{ FAH }
&=&
\frac{1}{2} \cdot 8 \cdot 10 \cdot \frac{3\sqrt{7} }{8} \\
&=&
15\sqrt{7}
\end{eqnarray}となります。
【解答】
アイ:12
ウエ:18
オカキ:157
【問題】
次に、$\angle\mathrm{ AFH }$の二等分線と辺AHの交点をP、$\angle\mathrm{ FAH }$に二等分線と辺FHの交点をQ、線分FPと線分AQの交点をRとする。このとき、Rは三角形AFHの[ク]である。次の0~2のうちから[ク]に当てはまるものを一つ選べ。0: 重心、 1: 外心、 2: 内心
(補足説明:三角形において、その外接円の中心を外心、その内接円の中心を内心という。)
【解説】
図は次のようになります。
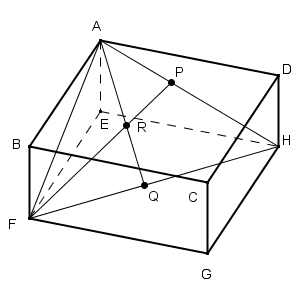
角の二等分線の交点は、その三角形の内接円の中心になるので、Rは三角形AFHの内心になります。
【解答】
ク:2
【問題】
また、$\mathrm{ AP }=[ケ]$であり、したがって、\[ \mathrm{ PF }:\mathrm{ PR } = [コ]:1 \]となる。
【解説】
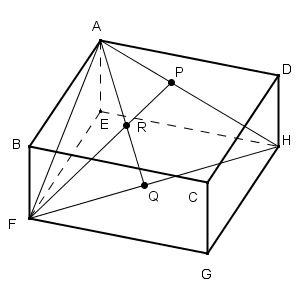
FPが$\angle\mathrm{ AFH }$の二等分線なので、$\mathrm{ AF }:\mathrm{ HF }=\mathrm{ AP }:\mathrm{ PH }$となります。$\mathrm{ AF }:\mathrm{ HF }=8:12=2:3$なので、
\begin{eqnarray}
\mathrm{ AP }=\frac{2}{5}\mathrm{ AH }=4
\end{eqnarray}となります。
また、ARは$\angle\mathrm{ FAP }$の二等分線なので、なので、$\mathrm{ AF }:\mathrm{ AP }=\mathrm{ FR }:\mathrm{ PR }$となります。$\mathrm{ AF }:\mathrm{ AP }=8:4=2:1$なので、$\mathrm{ FR }:\mathrm{ PR }=2:1$となります。よって、$\mathrm{ PF }:\mathrm{ PR }=3:1$がわかります。
【解答】
ケ:4
コ:3
【問題】
さらに、四面体EAPRの体積は$[サ]\sqrt{[シ]}$である。
【解説】

四面体EAPRをいきなり求めるのは難しいです。なので、わかりやすいものを利用して求めることを考えましょう。
四面体EAFHを考えます。この四面体でAFHを底面と見ると、このときの高さは、四面体EAPRで三角形APRを底面と見たときの高さと一致します。よって、四面体EAFHの体積を出し、底面の三角形の面積の比を使えば、四面体EAPRの体積を求めることができるようになります。
$\mathrm{ PF }:\mathrm{ PR }=3:1$なので、三角形APRの面積は、三角形AFPの面積の$\frac{1}{3}$です。また、$\mathrm{ AP }:\mathrm{ PH }=2:3$なので、三角形APRの面積は三角形AFHの面積の\[\frac{1}{3}\times\frac{2}{5}=\frac{2}{15}\]倍であることがわかります。
一方、四面体EAFHの体積は
\begin{eqnarray}
\frac{1}{3} \mathrm{ AE } \cdot \frac{1}{2} \cdot \mathrm{ EF }\cdot \mathrm{ EH }
\end{eqnarray}であり、FHを求めたときに計算した通り、$\mathrm{ EF }=\sqrt{54}$、$\mathrm{ EH } =\sqrt{90}$なので、
\begin{eqnarray}
\frac{1}{3} \sqrt{10} \cdot \frac{1}{2} \cdot 3\sqrt{6} \cdot 3\sqrt{10}
&=&
\frac{90\sqrt{6} }{6} \\
&=&
15\sqrt{6} \\
\end{eqnarray}となります。よって、四面体EAPRの体積は\[15\sqrt{6}\times \frac{2}{15}=2\sqrt{6}\]と求められます。
【解答】
サシ:26